Papa, ce sont seulement des idiots qui sont absolument certains d’eux-mêmes.
Louise, 5 ans
Disclaimer : cet article est destiné à ceux et celles qui ont plus d’habitude d’utiliser les mots comme « boosting » et « bagging » que « probabilité conditionnelle » et « théoreme de Bayes », i.e. aux Data Scientistes dans le domaine de Machine Learning (ML-ers).
Suite aux interprétations de la « probabilité » que nous avons déjà vu (ici, ici et ici), aujourd’hui je voudrais parler d’un autre classe de probabilités – Ap.
Durant mes cours de proba à l’école j’ai toujours eu du mal avec mon professeur car je posait des « mauvaises » questions. Par exemple : « pour ce problème est-ce que je peux imaginer plusieurs mondes avec des caractéristiques différentes et y appliquer la probabilité ? » C’est seulement relativement récemment j’ai appris que la question n’était pas finalement si mauvaise…
Prenons l’exemple classique d’une monnaie que nous allons jeter et pour laquelle nous voulons prédire la probabilité de « pile » ou de « face ». Si la monnaie ne semble pas avoir des défects évidents, nous avons vu que la meilleure réponse que nous pouvons donner est : P(face|aucune information concernant monnaie)=0,5. Comment pouvons-nous donner la prédiction pour le deuxièmes ou troisième expérience ?
Une autre chose qui m’a préoccupée c’est la « certitude » de ma prédiction. Autrement dit, pour la monnaie je suis « assez certain » que la probabilité de « pile » ou de « face » sera autour de 0,5 même après l’expérimentation. Par contre, si on me demande un chiffrage d’un projet et la probabilité qu’on ne le dépassera pas, je peux statuer la probabilité de 0,5 pour un chiffrage « juste » (ou 0,95 si j’ai pris de la marge), mais mes estimations sont moins « certaines » que dans le cas de la monnaie. C’est comme si les chiffres ont encore une dimension…

Si vous créez un réseau de neurones pour la classification d’images, prédiction d’évènements, etc, vous recevez qu’un seul chiffre de la probabilité de la prédiction (ou un vecteur) et assez certainement on ne capte pas notre « incertitude » concernant ce chiffre. Probablement, nous perdons une partie d’information.
Personnellement, j’ai besoin de « visualiser » les formules, donc voici ce qu’on peut faire (de façon visuel) pour analyser ce problème :
- nous pouvons dire que nous existons dans l’un des mondes avec les propriétés connues,
- dans chaque monde il y a un monnaie avec ces propriétés,
- nous ne savons pas, dans quel monde probable on existe,
- mais on peut assigner la distribution de probabilités à ces mondes (i.e. dire, quel monde est plus ou moins probable).
Si je me base sur mon expérience « normal » précèdent, mon modèle mental pour la monnaie doit être le suivant :
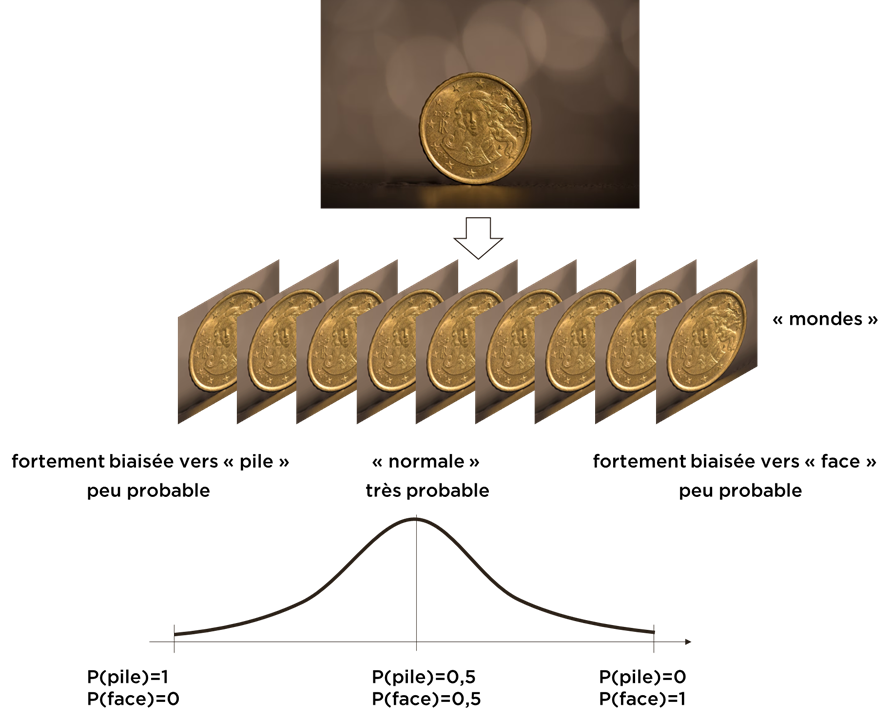
Ici j’ai mis plus de « densité » sur le cas où la monnaie est « non-biaisée » et moins – sur les cas de la monnaie « biaisée » car cela correspond le mieux à mon expérience précédent (même si je ne connais rien concernant la pièce en question).
Par contre, je peux savoir que la monnaie est biaisée (ex. on me l’a donné durant une soirée pour faire une blague), mais je ne l’avais pas examinée et dans ce cas ma « distribution des mondes » sera suivante :
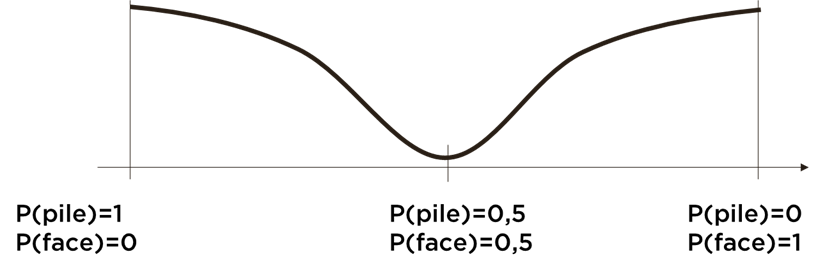
Ici la distribution est inversée car je suis assez certain que la monnaie est « biaisée », mais je n’ai pas plus d’information…
Nous venons d’introduire la probabilité Ap (elle n’a pas de meilleur nom, à ma connaissance), i.e. la probabilité de la probabilité.
Dès maintenant nous pouvons faire plusieurs choses :
- mesurer notre incertitude de la prédiction (ex. avec variance de Ap) :
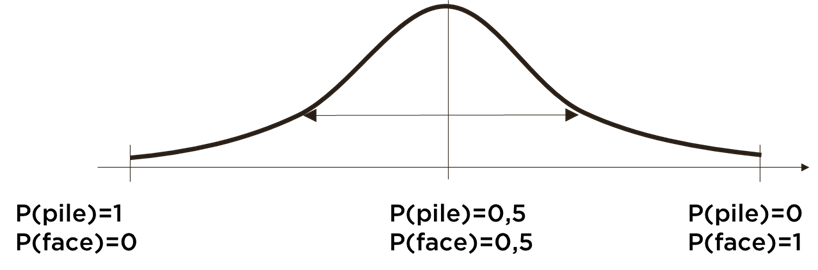
- apprendre sur l’expérience, i.e. si nous jetons la monnaie N fois, nous pouvons mettre à jour la fonction Ap en utilisant la loi de Bayes, par exemple :

- toujours faire nos prédictions (i.e. « collapser » la fonction en chiffre avec la formule d’espérance mathématique) :
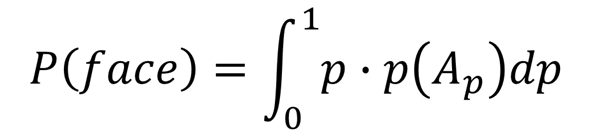
A noter que pour les deux monnaies – « non-biaisée » et « biaisée » si nous devons faire une prédiction pour la première expérience, elle sera la même : P(pile)=P(face)=0,5 car les deux Ap sont symétriques autour de 0,5, mais les manières de faire la deuxième prédiction pour ces monnaies seront très différentes car après la première expérience avec la monnaie les Ap se changeront différemment.
La « certitude absolue » (i.e. P(pile)=1 soit P(face)=1) correspond dans notre notation à Ap égale à une delta-fonction de Dirac (et c’est le seul cas où nous ne pouvons plus rien apprendre par la suite) :
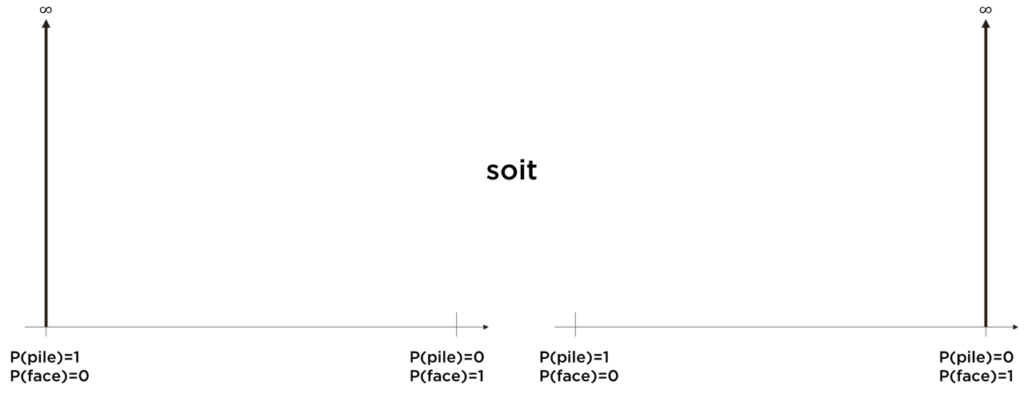
Suite pour les ratios
Dans l’article précédent nous avons parlé concernant représentations équivalentes de la probabilité. L’une des représentations est utilisée dans des jeux, par exemple la phrase « vos chances sont 3 contre 4 » veut dire que pour les 3 personnes qui ont parié « pour » il y a 4 qui ont parié « contre ». I.e. si vous vous basez sur la sagesse de la foule, vos chances de gagner sont 3/(3+4) = 3/7 ~ 0,429.
Est-ce que « 3 contre 4 » est équivalent à « 30 contre 40 » ? La probabilité semble être la même car 30/(30+40) = 3/7 = 3/(3+4), mais dans le cas de « 30 contre 40 » quelque chose se change – il y a bien plus d’opinions, i.e. notre « incertitude » concernant les chances de gagner se diminue.
Nous pouvons dans le cas le plus simple modéliser cette connaissance avec une distribution Ap~Beta, au moins pour expliquer ce point. Cette distribution a deux paramètres : a et b qui correspondent aux nombres de mises « pour » et « contre » respectivement.
Voici comment cette distribution (Beta) se comporte :
- l’espérance de Beta(a,b) = a/(a+b), ce que correspond à notre résultat précédent ;
- la variance de Beta se diminue avec l’augmentation de valeurs a et b :
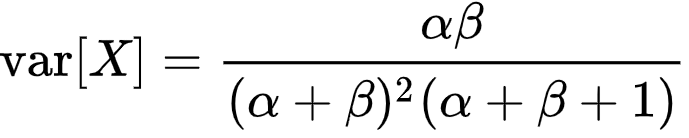

Autrement dit, la distribution devient de plus en plus « pointue » avec l’augmentation des paramètres a et b. Par exemple, voici les graphiques de Beta(3,4) contre Beta(30,40) :

Les deux ont la même espérance ~0,429, mais pas du tout la même variance.
Note. A ma connaissance, c’est l’une des raisons, pourquoi des banques préfèrent l’investissement vers une multitude de projets « plus petits » à l’investissement vers « un seul grand projet », même si les « risques » peuvent être comparables. Si une banque peut se protéger contre les pertes prédictibles qui ne dépasseront presque jamais une certaine somme maximale, une grande perte peut l’affecter sérieusement.
Utilité pour ML
Cette histoire est bien intéressante, mais les ML-ers doivent se demander comment ça peut améliorer leur vie (je ne pense pas que j’ai réussi de convertir quelqu’un de passer vers le côté lumineux de la force).
Les ML-ers vont voir une certaine ressemblance de cette technique aux techniques de l’apprentissage ensembliste (AE, Ensemble Learning) où chaque modèle représente un « monde » assez indépendant d’autres. Nous savons aujourd’hui que des ensembles sont souvent meilleurs que des modèles qui les composent. En prenant la valeur agrégée d’ensemble (prédiction moyenne, par exemple), nous approximons l’intégrale de la probabilité Ap et donc la vraie probabilité. J’espère que mon hypothèse concernant les raisons de bon fonctionnement d’AE n’est pas pire que les autres que vous avez rencontré.
Sinon, cette vision est également constructive car voici comment vous pouvez faire un upgrade à l’algorithme « lambda » :
- prenez le meilleur algorithme dans votre arsenal ;
- via l’algorithme d’optimisation trouvez les paramètres (et hyperparamètres) pour la « meilleure solution » ;
- faites varier les paramètres de l’algorithme (sans hyperparamètres) avec MCMC (Markov Chain Monte Carlo) – cela donnera plusieurs « samples » de la distribution des « mondes »;
- obtenez N modèles avec MCMC – et prenez la moyenne en tant que la prédiction finale (vous pourrez aussi approximativement estimer l’incertitude de la prédiction).
Cela ressemble à la méthode de « bagging », mais notre approche est plus structurée et plus correcte de point de vu de La Théorie. Pour les réseaux de neurones, Googlez « Bayesian Neural Network ».
C’est déjà pas mal, je pense, le seul problème est que nous pouvons faire encore mieux, mais pour cela il faudra inventer l’algorithme meilleur que notre « lambda ».
Conclusion
La théorie de probabilités cache des merveilles. Même si ML est à la mode aujourd’hui (à cause des résultats incroyables dans certains domaines, tels que la reconnaissance d’images, NLP, etc), la théorie de probabilités n’a pas prononcé son dernier mot.
Bonne santé à vous et à vos modèles.