Aujourd’hui je vous propose de tenter de résoudre un problème algorithmique de même type qu’on propose pendent les entretiens chez Google, Amazon, <you name it>.

Si vous voulez essayer de trouver la solution vous-mêmes, ne lisez pas l’article jusqu’à la fin car à la fin il y aura des spoilers (aka solutions).

Problème

Il existe un robot qui habite sur une grille rectangulaire de taille M x N et au moment t0 il se trouve dans le carré avec les coordonnées (0,0) :

Le robot peut se déplacer uniquement en haut ou à droite, mais il ne peut pas faire des pas en bas ou à gauche. Le but du robot est d’arriver dans le carré en haut à droite de la grille (banque).

Par exemple, voici l’un des chemins possibles :

Votre but est de calculer le nombre de chemins différents que le robot peut prendre pour arriver à la banque.

Par exemple, voici deux chemins différents sur une grille 6 x 4 :

Entrée d’algorithme : deux chiffres M et N.

Sortie d’algorithme : nombre de chemins possibles.

A vous d’essayer. Ajoutez vos programmes dans les commentaires sur LinkedIn.

Solution 1.

Nous pouvons remarquer qu’il y a deux possibilités pour arriver à la banque : le dernier pas peut être fait soit depuis le carré à gauche de la banque, soit depuis le carré sous la banque et les chemins qui passent par ses carrés seront bien évidemment différents…

…mais c’est comme si nous avons deux banques – un à gauche et l’autre – en bas de la banque initiale…

Conclusion : le problème peut être résolu avec une fonction récursive qui va juste additionner le nombre de chemins :

Nous avons besoin juste d’arrêter la récursion à certain moment, mais nous pouvons remarquer que si notre robot habite dans un tuyau (i.e. M=1 ou N=1) il a qu’un seul chemin à prendre, i.e.

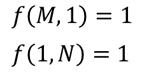
Bravo ! Nous avons résolu le problème en 6 lignes de code (j’utilise Python ici, désolé) :

def calc(a,b) :
  if a==1 :
      return 1
  if b==1 :
      return 1
  return calc(a-1,b)+calc(a,b-1)

Discussion

Si on lance vraiment le code, on verra rapidement ses limites… en fait, probablement notre fonction calc lancée avec paramètres 20, 20 ne se finira jamais.

Pourquoi ? Même si la solution est correcte, notre compilateur ne peut pas tout optimiser pour nous dans ce cas et la complexité de l’algorithme sera exponentielle (i.e. avec l’augmentation de M et N par 1, le calcule prendra 2x plus de temps pour se terminer).

Voici pourquoi: si on affiche le nombre d’exécutions de notre fonction « calc » pour chaque paire de valeurs, nous allons obtenir le schéma suivant :

• calc (6,4) est à exécuter une fois,
• donc on exécute calc(5,4) et calc(6,3),
• mais chacune de ses fonctions exécutera calc(5,3), donc calc(5,3) sera exécutée 2 fois,
• de même calc(4,2) sera exécutée au moins 4 fois et calc(3,1) – au moins 8 fois.

Cela ne change rien pour les M et N relativement petits, mais pour M et N plus importants, notre fonction ne se finira jamais… Comment pouvons-nous l’améliorer ?

Solution 2.

Si vous avez entendu les expressions comme « pure function » et « dynamic programming », probablement vous êtes arrivés rapidement à cette solution.

L’idée est la suivante: nous pouvons ne pas recalculer notre fonction à chaque fois quand nous avons besoin de sa valeur car nous pouvons mettre les résultats précédents en « cache ». Nous pouvons même faire mieux : exécuter le calcul dans un autre sens – en montant de f(1,1) jusqu’à f(M,N) et en sauvegardant les résultats intermédiaires dans une matrice :

La solution naïve utilisera O(M*N) de mémoire, mais le temps de calcul baissera d’exponentiel à quadratique, i.e. O(M*N) aussi :

def calc2(a,b) :
  if (a==1) or (b==1) :
      return 1
  M = [[1 for x in range(a)] for y in range(b)]
  for x in range(a-1) :
      for y in range(b-1) :
          M[y+1][x+1] = M[y][x+1] + M[y+1][x]
  return M[b-1][a-1]

Par la suite on peut remarquer qu’on n’a pas besoin d’autant de mémoire car après un passage d’algorithme on n’utilise que deux dernières lignes (ou colonnes) de la matrice (ça dépend d’ordre de boucles). I.e. nous pouvons obtenir un algorithme linéaire en mémoire O(min(M,N)) et toujours « quadratique » en temps O(M*N).

Discussion

Notre algorithme n’a pas vraiment d’entrées (sauf les dimensions), donc l’utilisation de programmation dynamique est un « overkill ». De plus, je voudrais calculer le nombre des chemins pour M=N=10000.

Solution 3.

Prenons notre matrice de résultats et tournons la un peu :

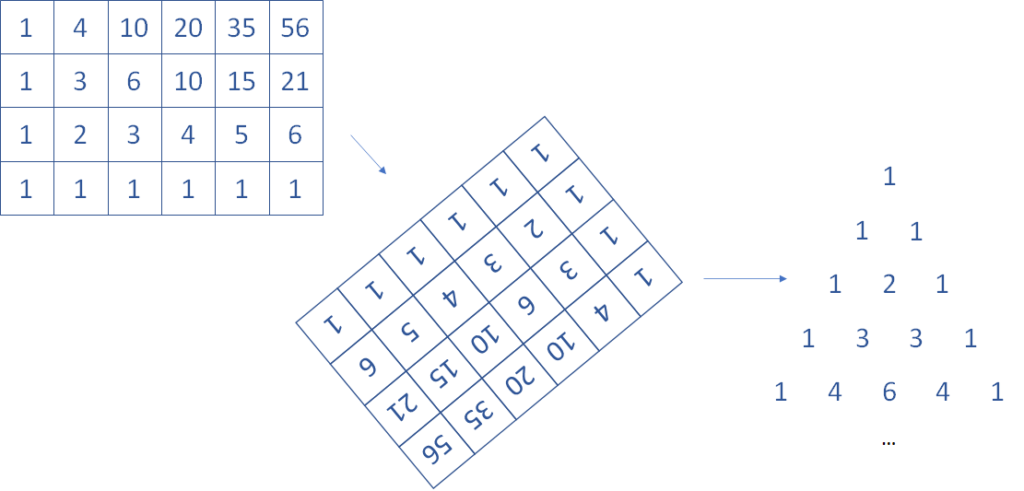
Je me suis permis d’extraire les chiffres de la matrice et les mettre à côté… c’est un « triangle de Pascal » (même si ce n’est pas Blaise Pascal qui l’avait découvert).

Autrement, nous pouvons voir la dépendance fonctionnelle si nous imaginons chaque chemin comme une programme pour le robot :

Chaque telle programme aura la longueur de (M+N-2), il y aura (M-1) pas à droite et (N-1) pas en haut… donc le nombre des chemins est égal à

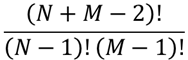
Pourquoi ? Voici le processus qui génère les programmes pour le robot :

La fonction en Python se simplifie (attention à « // » pour manipuler l’arithmétique longue) :

import math
def calc3(a,b) :
    return math.factorial(a+b-2)//math.factorial(a-1)//math.factorial(b-1)

Nous pouvons encore jouer avec l’optimisation de calcul pour les M et N très importants (via la fonction log-gamma), mais je peux déjà calculer le nombre de chemins dans un carré 10’000 x 10’000 et je vais m’arrêter ici :

Conclusion

Je ne sais pas ce que testent les sociétés qui proposent ce genre de problèmes durant ses entretiens car dans 99% pour écrire une application il faut juste connaitre la différence entre un algorithme quadratique et celui avec une complexité de O(N*log(N))… mais visiblement ni Google ni Amazon ne veulent plus des « coders simples » que nous pouvons maintenant remplacer à 50% avec un réseau de neurones :

…ou probablement ils savent que dans chaque bon coder vit un mathématicien ?

Bonne santé à vous et à votre code !