– Quelle est la probabilité de rencontrer un dinosaure dans la rue ?
– Un sur deux.
– ???
– Soit je vais le rencontrer, soit non.
Aujourd’hui je voudrais vous présenter le théorème qui m’a choqué. Je suis certain qu’il sera très utile pour les Data Scientistes, mais également ce théorème ouvrira les yeux à beaucoup d’autres proffessionnels.
Je crois que ce théorème est aujourd’hui plus important que jamais à cause des certaines idées qui sont souvent publiées sur LinkedIn : « Machine Learning est plus puissant que les probabilités », « Vers les algorithmes plus avancés – probabilité n’arrive plus à résoudre les problèmes »… C’est juste faux.
A l’école
Comment nous apprenons la théorie de probabilités à l’école « lambda » ?
Probabilité est un certain chiffre est voici les règles comment le manipuler :
Quand je jette une monnaie parfaite, la probabilité de « face » est 0,5.
D’où viennent ces règles ? Qui dit que la théorie de probabilités est un outil puissant ? Kolmogorov ? Geoffrey Hinton dit qu’il faut faire les réseaux de neurones !
Au final même les meilleurs élèves sortants d’écoles ne peuvent pas comprendre même la provenance de la fonction d’erreur de réseau de neurones (surprise ! vient de la théorie de probabilités en fait).
Je voudrais vous proposer un petit revue d’un théorème qui peut vous choquer et changer votre vision.
Boole
Au début il y avait la logique. La logique mathématique. Vous l’utilisez chaque jour quand vous parlez avec votre enfant / votre manageur / votre professeur. Elle est très simple, mais très puissante. Elle porte le nom de l’algèbre de Boole (algèbre booléenne) à l’honneur de ce gentleman, George Boole :

Voici les bases dont nous allons avoir besoin :
- comme d’habitude en mathématique nous allons utiliser les lettres A, B, C, …, X, Y, Z pour noter des objets dont on parle ;
- par contre, au lieu de parler des chiffres, on va parler d’expressions : « j’ai fait mes devoirs », « le deadline s’approche » ;
- pour chaque expression on peut dire si le contenu est vrai ou faux ;
- on se permet quelques opérations :
- et : « j’ai fait mes devoirs » et « j’ai sorti les poubelles » – ça sera vrai seulement si les deux expressions sont vrais, i.e. si j’ai fait les devoirs, mais je n’ai pas sorti les poubelles, l’ensemble reste faux,
- ou : « j’ai fait mes devoirs » ou « j’ai sorti les poubelles » – ça sera vrai si au moins l’une des deux est vrai (ou les deux en même temps – pas de problème avec ça),
- ne : ne « j’ai sorti les poubelles » – ça sera vrai que si l’expression est fausse (i.e. je n’ai pas sorti les poubelles).
En gros, c’est presque tout. Voici comment on peur présenter cela plus « mathématiquement » (a noter que je vais utiliser le français, mais les mathématiciens utilisent plein d’autres symboles) :
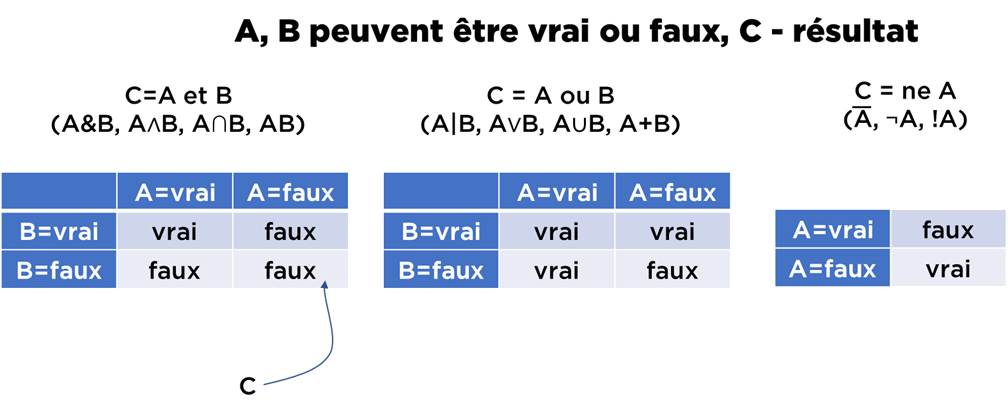
L’un des résultats importants de la logique booléenne est qu’il suffit de définir deux opérations (« et » et « ne », par exemple) pour construire une expression aussi complexe qu’on veut à partir d’expressions plus simples. Tout est à cause de la règle suivante :
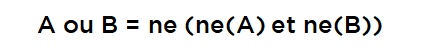
…vous pouvez la vérifier juste en mettant les quatre valeurs possibles et en faisant le calcul.
Bien évidemment, il y a un tas d’autres « règles », par exemple :

Nous allons ajouter encore une notation pour dire « à condition que… » :

Ici on ne parle plus de A ou de B – on parle de nouveau objet – A conditionné par B. Par exemple, « demain je vais faire mes devoirs à la condition que j’aurai du temps ». Si A = « demain je vais faire les devoirs » et B = « j’aurai du temps », dans ce cas, notre expression peut être écrite comme A|B (ce n’est pas « ou » – c’est bien la condition).
Tout ce qu’il faut savoir concernant cette opération est qu’on a le droit de réarranger les conditions de manière suivante :
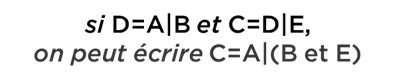
Si ce n’est pas évident, comparez :
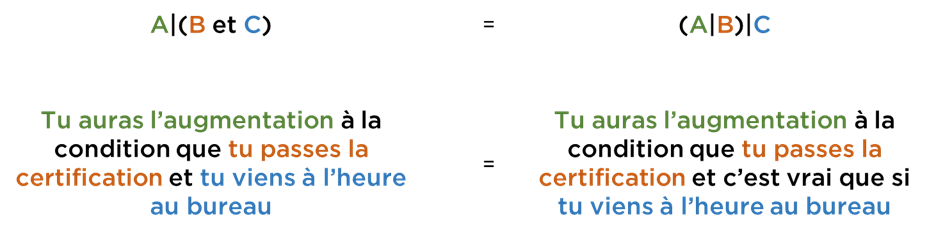
Essayez de vous convaincre que tout ça ne contredit pas votre « bon sens » car toute mathématique (et IT) se base sur ce genre de la logique. Tout ce que vous pouvez décrire avec la logique de Boole est « imbattable », i.e. vous ne pouvez pas faire une meilleure preuve qu’en faisant une manipulation mathématique. C’est juste le seul moyen pour raisonner logiquement. Le problème est que dans la vraie vie nous ne savons pas si A, B, C sont vrai ou faux…
Cox et Jaynes
Cox (et puis Jaynes) n’ont pas découvert la théorie de probabilités, mais ils ont pu trouver un moyen pour prouver que la théorie de probabilités était le seul moyen pour faire une extension de la logique de Boole (i.e. tout ce qui est fait avec un modèle probabiliste correct ne peut pas être fait encore mieux si vous cherchez une réponse raisonnable).

Comment est-il possible de prouver qu’il n’existe pas d’autres moyens pour résoudre un tas de problèmes, alors que les problèmes ne sont pas définis ? C’est très mystérieux. C’est comme si je dis que Python est le meilleur moyen pour programmer, peu importe quel programme et il n’y aura plus jamais d’autres langages de programmation plus avancés.

Voici les inputs pour le théorème :
- nous voulons faire une extension de la logique de Boole (car c’est la seule logique imbattable qui existe depuis les temps d’Aristote, en fait),
- au lieu d’utiliser les valeurs Vrai ou Faux, nous allons utiliser les chiffres (réels) pour décrire notre « niveau de certitude » que quelque chose est vrai ou faux,
- nous voulons que le résultat ne soit pas contradictoire à notre « bon sens »,
- nous voulons que le résultat (notre « langage ») soit « correct » (sans contradictions), i.e. :
- si nous avons un moyen pour raisonner différemment, les différents raisonnements doivent donner le même résultat ;
- nous allons utiliser toute information disponible et n’ignorer rien du tout ;
- les résultats équivalents doivent être représentés par les mêmes chiffres.

Si vous êtes Ok avec les entrées et la suite, vous allez devoir croire aux résultats, n’est pas ? Vérifiez que c’est Ok pour l’instant.
Maintenant nous allons imaginer ce que veut dire vivre dans le monde d’incertitude. Supposons que le le chef dit « je suis certain qu’il faut finir ce projet à temps et ne pas dépasser le budget, sinon nous pouvons mettre les clés sous la porte » et puis « dis-moi, tu es certain qu’on peut le faire ? ». A vous donc d’estimer :

Supposons que vous estimez que vous êtes très certains que le projet sera fini à temps, mais moins certains qu’il ne dépasse pas le budget (je vous laisse choisir les chiffres quelconques pour représenter votre certitude). Quelle doit être la certitude d’ensemble d’expression ? Faut-il s’aligner avec la proba ou il y a mieux ?..
C’était un exemple. Revenons vers le théorème. Le premier pas de la preuve c’est de remarquer que nous avons besoin d’obtenir les expressions seulement pour les opérations « et » et « ne » car on pourra déduire les autres (« ou », « xor », « nand », etc) en utilisant les expressions de l’algèbre booléenne.
Commençons par l’opération « et », i.e. C = A et B. Ce qu’on veut c’est de pouvoir trouver une expression pour C :

Nous allons chercher l’expression pour « et » en forme d’une fonction inconnue et voyons si nous pouvons la trouver. En réalité pour le faire, les valeurs de certitude(A) et certitude(B) peuvent ne pas être suffisantes car il faut aussi savoir, comment A impacte B et vice versa (probablement C est une tautologie), donc on ajoute A|B (A à la condition de B) et B|A (B à la condition de A) :

Pour « sentir » cet argument, revenons vers notre exemple. Afin d’estimer la probabilité de succès de notre projet, nous avons regardé l’historique d’anciens projets de notre entreprise. Nous avons découvert que 50% de projets se sont terminés sans dépasser le deadline et 50% n’ont pas dépassé le budget. En revanche, ces deux chiffres ne sont pas suffisants afin d’estimer le résultat. Car il peut se passer que tous les projets qui se sont terminés à temps ont dépassé le budget et tous les projets qui n’ont pas dépassé pas le budget, ont dépassé le déadline (autrement dit, les chances de A « et » B sont proches à 0,00…). Donc même si les chances sont 0,5 et 0,5, les chances de A « et » B sont très petites :

Est-ce qu’on pourra trouver cette fonction inconnue ? Est-ce que la fonction est unique ou on a le choix ?
En fait on demande beaucoup trop de choses à estimer – on n’a pas besoin d’utiliser tous les quatre paramètres. Comment choisir que ce qu’il nous faut ? Heureusement pour nous, cet exercice a été déjà fait en utilisant le bon sens et il a été démontré que la certitude de C peut être représentée de deux manières différentes seulement (qui sont symétriques) :

Mais comment c’était fait ?
Pour vous donner une idée, nous allons prendre un exemple. Il existe au total 16 différents moyens pour choisir les paramètres (2*2*2*2 : prendre ou pas la certitude de A, B, A|B ou B|A). Il faut vérifier toutes configurations pour prouver qu’il n’existe que deux valables – nous n’allons pas le faire, nous allons juste essayer un cas.
Supposons que la fonction qu’on cherche dépend de certitude(A) et de certitude(A|B) seulement [j’ai inversé les lettres de la bonne réponse, vous avez remarqué ?] et prouvons que ce n’est pas compatible avec le bon sens, i.e. il nous manque de l’information. En effet, si B est impossible, l’expression (A et B) doit également être impossible. Prenons un exemple A = « demain je m’achète du pain » et B = « je gagne au Loto » :
certitude(acheter du pain) – haute,
certitude(acheter du pain si gagne au Loto) – haute (mais pourquoi pas – il faut mettre le caviar sur quelque chose),
…donc, si tout se passe bien, la certitude(demain je m’achète du pain et je gagne au Loto) doit aussi être haute, mais ce n’est pas le cas… donc on doit éliminer cette forme – elle n’est pas complète.
La fonction de conversion de certitudes est toujours inconnue pour nous, mais en connaissant les paramètres on peut essayer de la trouver. Si on considère une expression plus complexe (A « et » B « et » C), nous allons pouvoir trouver l’équation dont nous avons besoin :

Autrement dit, si une telle fonction existe, elle doit avoir une forme très spéciale pour respecter la règle de l’algèbre de Boole (pour x, y et z presque quelconques) :

Heureusement pour nous, la solution générale pour cette équation est connue – il existe infiniment beaucoup de fonctions comme ça, mais elles ont toutes la même forme. Choisissez n’importe quelle fonction g(x) – et vous allez trouver que la fonction suivante respecte toutes nos conditions (ici g-1 est la fonction inverse) :

Par exemple, je peux prendre g(x) = ex ou g(x) = x et obtenir les formes suivantes :

Nous avons cherché une seule fonction pour une seule théorie pour calculer les « certitudes », mais on en a trouvé infiniment beaucoup… Attendez, mais ces fonctions sont toutes pareilles à delta d’une transformation (fonction g). Je vous rappelle qu’au début nous avons cherché la valeur d’une certaine certitude. Maintenant je vous propose au lieu de chercher cette certitude, chercher plutôt g(certitude(A)). Redéfinissons de façon suivante :

Si on appelle ce « P » la « probabilité », nous obtiendrons l’une des formules connues en théorie de probabilités – probabilité conditionnelle. Depuis cette formule on peut, par exemple, obtenir le théorème de Bayes. Le plus étonant : nous n’avons utilisé aucune définition de la théorie de probabilités – juste la mathématique pour faire une extension de la logique booléenne et du bon sens. Autrement dit, si une logique « incertaine » imbattable existe, la seule solution possible est la théorie de probabilités. Et on n’a plus besoin d’axiomes de Kolmogorov – on peut déduire les règles autrement.
Note.
En effet, il existe un nombre de présentations « utiles » de niveau de certitude et la « probabilité » n’est pas la seule. Par exemple, la certitude peut être représentée comme un ratio des chances. Cette méthode est souvent utilisée dans les jeux : à un hippodrome on vous dit: « vous avez les chances 3 contre 5 ». Alors la probabilité de gagner est P(A) = 3/(3+5) = 3/8. Si on vous dit : « vos chances sont 4 contre 4 », la probabilité de gagner est P(A) = 4/(4+4) = 0,5 (incertitude absolue).
Vous pouvez prendre le logarithme du ratio de chances et passer à l’échelle logarithmique (mesuré en bels ou décibels). L’incertitude absolue sur une telle échelle est égale à 0, alors que la certitude est plus ou moins infinie. L’échelle logarithmique est utile pour faire un calcul avec une multitude de facteurs – par exemple le filtre anti-SPAM utilise cette technique pour estimer les chances que le nouveau mail fait partie de SPAM ou pas.
| P(A) | Ratio | Logarithme(Ratio) |
|---|---|---|
| 0 | 0 | -∞ |
| 0,5 | 1 | 0 |
| 0,8 | 4 | 1,386… |
| 1,0 | +∞ | +∞ |
De ce point de vu, la « probabilité » est juste une représentation « normalisée » parmi multitude d’autres équivalentes et convertibles – cela colle parfaitement avec nos résultats.
Attendez, ce n’est pas tout. Est-ce que la valeur de P peut être supérieure à 1 ou inferieure à 0 ? Peut-être 3 ? 7 ?
Nous pouvons faire quelques expérimentations mentales et voir que si A est vrai, P(A) doit être égale à 1 justement à cause du fait que la multiplication par 1 ne change pas le résultat (comme A et B = B si A est toujours vrai). En raisonnant de même manière, P(A)=0 si A est impossible.
Il est également possible de démontrer que « ne » (négation) doit respecter un tas d’équations :

Cela donne encore une équation fonctionnelle pour la fonction de « négation » (pour x et y quelconques entre 0 et 1) :

…pour laquelle il existe une solution (en fait une multitude de solutions, dont une seule qui correspond à toutes conditions dont nous avons parlé) :
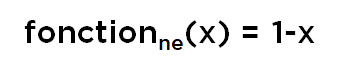
Autrement dit, nous avons déduit encore un résultat de la théorie de probabilités :
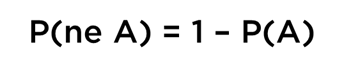
Une fois nous avons « et » et « ne », nous pouvons déduire le « ou » (essayez vous-mêmes, je donne le schéma) :

Pour la « mathématique », nous allons nous arrêter ici. Evidemment j’ai du jeter certains morceaux de calcul. Mon but était de convaincre ceux et celles qui n’ont pas entendu parler de ce théorème que :
- si vous pensez pouvoir faire mieux qu’un modèle probabiliste bien construit, vous perdez votre temps ;
- la théorie de probabilités peut ne rien avoir avec les sigma-algèbres et Kolmogorov – vous avez le droit de l’appliquer partout, même si vous raisonnez concernant les choses uniques et non-scientifiques (probabilité de tomber amoureux / certitude d’avoir vu le meilleur endroit dans le monde / etc).
Voici votre technique optimale pour résoudre les problèmes que vous pouvez « spécifier » plus ou moins bien.

Note. En fait, une monnaie a la probabilité de tomber « face » strictement égale à 0,5 si vous la jetez pour la première fois et elle n’a pas de défauts évidents. Ce n’est pas parce que la monnaie est « parfaite », mais à cause de fait que vous n’avez aucune information concernant la monnaie et vous ne pouvez pas l’obtenir. Ici la probabilité n’est pas la prédiction exacte du résultat, mais la meilleure prédiction possible en prenant en compte l’information que vous avez à votre disposition.
Pourquoi 0,5 ? Vous ne voyez aucune raison pour que la monnaie tombe plutôt « face » ou plutôt « pile », mais vous pensez que ça sera l’un ou l’autre, i.e. P(face)=P(pile), mais P(face)=P(ne pile).
Autrement dit, 1=P(face)+P(pile)=P(face)+P(face). 2*P(face)=1. P(face)=0,5=P(pile).
Plus précisément : P(face|aucune information)=0,5. Même chose pour les dinosaures. 🙂
Machine à laver
Depuis des années les machines à laver sont devenus plus « intelligentes ». Votre machine à laver utilise aussi un algorithme « incertain » pour décider si le cycle programmé peut être terminé ou pas. Autrement dit, la machine n’est jamais certaine concernant l’état des choses, pourtant elle arrive à finir le cycle à l’heure avec le résultat plus ou moins acceptable.
Par contre, au lieu d’utiliser la théorie de probabilités, la machine à laver utilise le « Fuzzy Logic », i.e. se base sur d’autres formules (par exemple, min/max) qui font aussi une certaine extension de la logique booléenne :

Que veut-il bien dire ? Fuzzy Logic fonctionne plus ou moins bien, mais dans son domaine seulement. Comme nous avons vu, elle est incertaine et fait une extension de la logique booléenne. Alors selon le théorème de Cox-Jaynes, Fuzzy Logic doit soit violer le bon sens, soit contenir des contradictions :
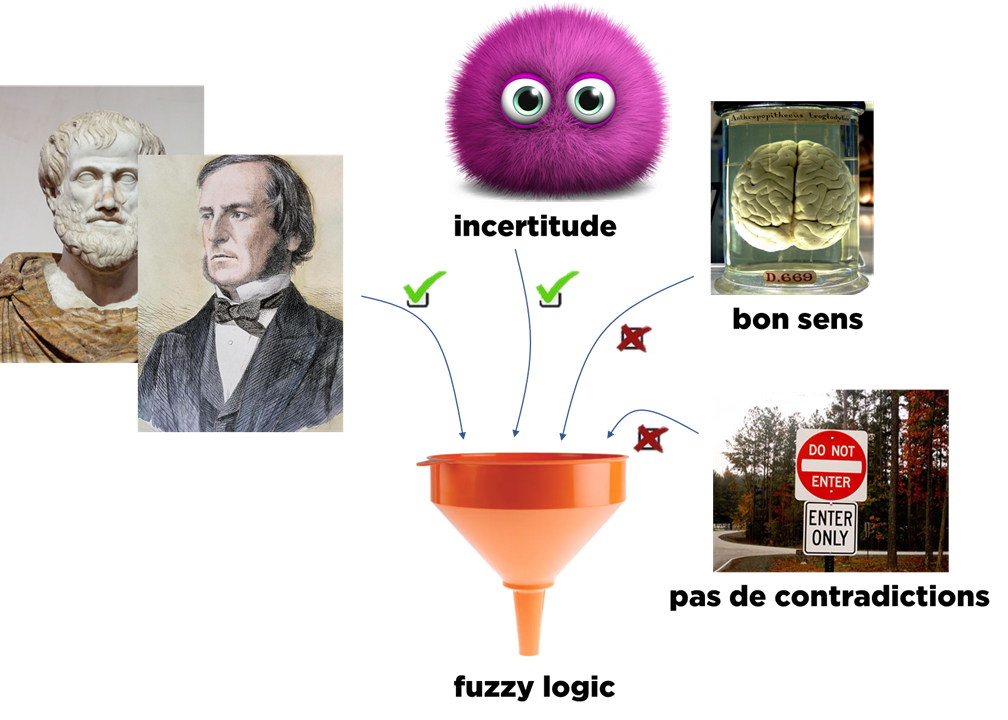
Et je vous prouverai que Fuzzy Logic contient bien des contradictions :

…je commence à comprendre où se cache la deuxième chaussette chaque fois après le lavage… elle est en superposition quantique.
Conclusion : si un jour une machine à laver utilisera les probabilités au lieu de la logique floue (Fuzzy Logic), elle fonctionnera mieux (en tout cas, pas pire qu’aujourd’hui).
Conclusion finale
Nous avons vu ensemble que la théorie de probabilités peut être utilisée hors de domaine de la science pure et elle restera un outil très puissant (plus puissant que les autres). Vous pouvez protester que les réseaux de neurones, XG Boost et les autres algorithmes de ML servent à la régression ou à la classification, alors qu’ici nous avons obtenu la théorie pour la manipulation d’expressions booléennes. Ce n’est pas bloquant car il se trouve que la même logique peut être appliquée aux problèmes de régression/classification/etc (probabilité que la fonction approche bien les données observées / probabilité que la fonction modélise bien le domaine). De plus, si nous connaissons la « physique » des processus que nous voulons modéliser, nous pouvons construire les algorithmes de la qualité « parfaite », i.e. ceux qui ne peuvent pas être améliorés sans introduire la nouvelle information précédemment inconnue.
Comment le résultat de Cox-Jaynes se colle avec le théorème « No free lunch » ? Il se trouve qu’il n’y a pas de contradiction. Dans le monde « rationnel », a théorie de probabilités gagne ! De plus, si pour un problème « black box » vous pouvez formuler « la probabilité que la fonction modélise bien le domaine », vous pouvez obtenir l’algorithme « parfait » pour ce problème en utilisant la théorie de probabilités.
Bonne santé à vous et à vos modèles !