Aujourd’hui, je voudrais vous proposer une expérience statistique simplissime et ludique : emmenez votre bout’chou faire promenade en ville, et, en naviguant d’une rue à l’autre, demandez lui prendre en photo des numéros de maison qu’il trouve jolis.
Une fois rentré à la maison, il est possible de faire un histogramme comme celui qu’on a fait avec ma fille : pour chaque premier chiffre du numéro d’un bâtiment (maison, immeuble), comptez le nombre d’occurrences (combien de numéros commencent par 1, combien par 2, etc).
Spoiler ! Voici notre résultat – et il est très étrange :

Posons nous la question suivante, est-il normal de retrouver plus de maisons avec le chiffre « 1 » au début. Ou non ?
Si vous avez remarqué la ligne bleue, ce n’est pas un hasard – ici j’ai superposé notre histogramme de numéros de maisons avec la mystérieuse loi de Benford.
Note. Benford a fait la promotion d’une loi étrange de distribution de certains chiffres, loi découverte bien auparavant par l’astronome S. Newcomb. La loi énonce que si vous mesurez certains processus qui peuvent donner des résultats de plusieurs ordres de magnitude de différence (tremblement de terre, somme dépensée dans un magasin, fréquences d’ondes), dans la représentation décimale le premier chiffre sera « 1 » dans 30% des cas, « 2 » – dans 18% des cas, …, « 9 » – dans moins de 5% des cas (sauf si vous achetez tout pour 99,99 Euro). C’est contre-intuitif, mais c’est comme ça. La loi fonctionne même en cas de changement d’unité de mesure, système (utilisez hexadécimal si vous voulez), etc…
La loi de Benford fonctionne si bien que dans domaine très sérieux comme la finances, elle est souvent appliquée à la détection des fraudes récurrentes. Votre honorable serviteur a eu de la chance de vérifier cette loi sur un dump de données d’une grande banque américain – et, devinez quoi ? Elle fonctionne à merveille !
La loi de Benford n’est en réalité pas si mystérieuse – c’est un symptôme de quelque chose avec une distribution proche de l’exponentielle, i.e. les processus naturels ont tendance à adopter des magnitudes limitées – et c’est seulement dans de rares cas qu’on peut tomber sur des valeurs extrêmes.
Pouvons-nous formaliser cette pensée ?
En fait, oui – dans les études statistiques c’est un problème récurrent – il nous faut assigner une distribution de probabilité, sans pour autant la connaître. Comment faire ? Un grand statisticien du XX siècle, E. T. Jaynes a proposé une méthode pour traiter cette situation – le principe d’entropie maximale (MaxEnt).

Je vous passe les détails pour le moment – appliquons dès maintenant ce principe à la numérotation des maisons. Ce que nous savons : le numéro est un entier, positif, « pas très grand » (a une espérance) et c’est tout … Le principe nous dit que la meilleure chose que nous pouvons faire c’est de modéliser les numéros pris par hasard par une distribution exponentielle. Cela expliquera l’apparition de la loi de Benford.
Un autre exemple – si je sais que la valeur mesurée peut être aussi positive que négative, mais elle a une « densité » autour de la moyenne, ça sera juste de prendre la loi normale.

Supposons que vous faites une geek party (vous avez le droit !) et vous proposez un jeu à vos invités – chacun doit choisir un chiffre entre 1 et 9 indépendamment l’un de l’autre, puis sans vous le dire, les invités doivent trouver une moyenne – et vous allez essayer de proposer un chiffre plus proche possible à la moyenne obtenue par les invités. Quel chiffre allez-vous choisir ? Pourquoi ?
J’espère que vous avez choisi cinq car c’est la moyenne la plus probable (sans prendre en compte la psychologie, etc).
De même manière, nous pouvons expliquer le principe de maximum d’entropie. Si nous prenons toutes distributions de probabilité avec certains critères imposés, la distribution « moyenne » (avec entropie maximale) sera la plus « juste ».
Afin de ne pas vous embêter, je vais juste faire une simulation en conditionnant par l’espérance (moyenne) :
#granularité de notre distribution
N = 50
#précision de notre distribution
Ess = 20
#mettons à zéro le réceptacle
frq = [0 for i in range(N)]
#mettons juste une condition sur la moyenne
m = 12
#et permettrons l'erreur sur la moyenne
err = 2
#simulation
for i in range (1500000) :
#simulation de la distribution complètement par hasard!
l = np.random.randint(0, N, Ess)
#on va rejeter la majorité de simulations,
#mais si la distribution a des propriétés souhaitées,
#on augmente notre réceptacle
if math.fabs(np.average(l) - m)<err :
for v in l:
frq[v] = frq[v]+1
plt.bar(x=[i for i in range(N)],height=frq)Le résultat est une exponentielle avec l’espérance autour de 12 (comme défini dans le code) :
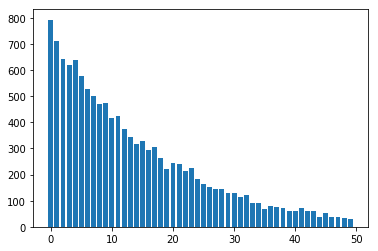
Même chose pour la condition sur l’espérance et la variance :
N = 50
Ess = 20
frq = [0 for i in range(N)]
m = 23
s = 7
err = 2
for i in range (1500000) :
l = np.random.randint(0, N, Ess)
if math.fabs(np.average(l) - m) < err and math.fabs(math.sqrt(np.var(l)) - s) < err :
for v in l:
frq[v] = frq[v]+1
plt.bar(x=[i for i in range(N)],height=frq)…donnera une distribution normale aka Gaussienne (dans la limite) :
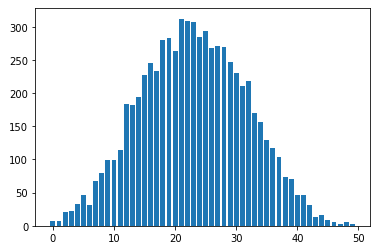
J’espère que vous comme moi sont étonnés par ce résultat. Ce qui est encore plus magique c’est que si vous utilisez ce résultat dans votre modèle statistique, il va fonctionner.
Comme dans notre expérience avec les maisons – je ne crois pas une seconde que la vraie distribution des numéros de bâtiment est exponentielle, mais elle a les propriétés proches à l’exponentielle – et ça suffit pour la plupart de modèles.
Question pour vous : pourquoi vous utilisez l’erreur normal dans les modèles de régression?
Bonne santé à vous et à vos systèmes !

