L’alchimie Machine Learning : No Free Lunch Theorem

Il est clair qu’un fait quelconque peut se généraliser d’une infinité de manières, et il s’agit de choisir, le choix ne peut être guidé que par des considérations de simplicité.

La Science et l’Hypothèse, H. Poincaré (1917)

Le théorème dont nous allons parler aujourd’hui concerne notre compréhension des techniques de Machine Learning. C’est pour ça qu’elle a créé autant de buzz et est si connue dans le milieu de ML. Le nom non-officiel « No Free Lunch Theorem » est assez générique et s’applique aux résultats obtenus par David H. Wolpert, ce qui nous intéresse ici, c’est la version initiale de 1995-1996 :

Faites attention : le théorème est tellement populaire qu’il est devenu folklorique avec de nombreux mythes autour.

Si on souhaite décrire la publication de 50 pages dans un petit article, il faut commencer par une question : si je vous donne deux points d’une courbe et je demande où se trouve le point entre les deux, quelle réponse vous semblera la plus pertinente ? Et pourquoi ?

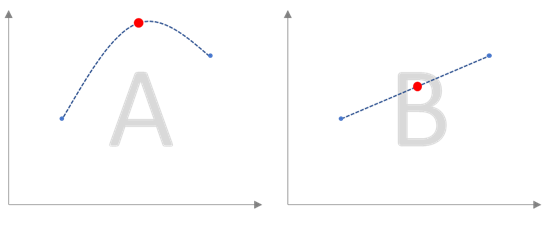
Si vous avez choisi la solution « B » (et vous avez bien fait) en l’accompagnant d’une explication du type « parce que c’est plus simple » ou « à cause de symétrie il n’y a pas de raison de la mettre plus haut ou plus bas » sans aucune précision sur la provenance de ces données ni les processus qui les ont générées, c’est à cause de votre « à priori » concernant le monde autour de nous – un monde où l’explication la plus « simple » est souvent la plus « vraie ». Sans cet « à priori », votre choix n’est plus valable – et vous ne pouvez plus trancher aussi facilement entre les deux propositions.

Pour être plus précis, l’idée de Monsieur Wolpert peut être décrite par la suite de conclusions suivantes (simplifiées) :

• Il est possible de montrer que chaque algorithme de ML a ses propres « prédilections » en terme de problèmes qu’il peut résoudre.
• Dans certains cas, l’algorithme sera « optimal » donc « imbattable ».
• Par contre, il existe toujours un autre cas où nous pouvons faire le « juste contraire » et obtenir un meilleur résultat.
• Le résultat est que « en général », il n’y a aucun algorithme meilleur que l’autre, il n’y a pas forcement de possibilité d’en choisir un seul, à condition que vous n’avez pas de connaissance « à priori » sur le domaine visé.

Cette suite de conclusions qui peut paraître banale propose néanmoins un argument concret contre « l’alchimie » Data Science – il ne suffit pas d’imaginer un algorithme et de montrer qu’il fonctionne mieux que d’autres dans un cas particulier car il y aura beaucoup d’autres cas « juste contraires ».

Par contre (et ici je voudrais revenir vers la citation au début d’article) si vous avez une bonne idée de contraintes de votre modèle (« à priori » sur le domaine), vous pouvez créer un algorithme qui sera « certainement meilleur » que tous les autres algorithmes existants. Cette vision est constructive – ce n’est pas juste la critique d’approches existantes, elle permet de construire les meilleurs algorithmes au lieu de copier-et-améliorer les algorithmes existants. L’exemple qui prouve que les algorithmes « idéales » peuvent fonctionner c’est le théorème de Cox (https://ithealth.io/un-algorithme-parfait/) qui propose une telle solution à condition que vous pouvez modéliser votre problème avec un modèle à la base de la logique.

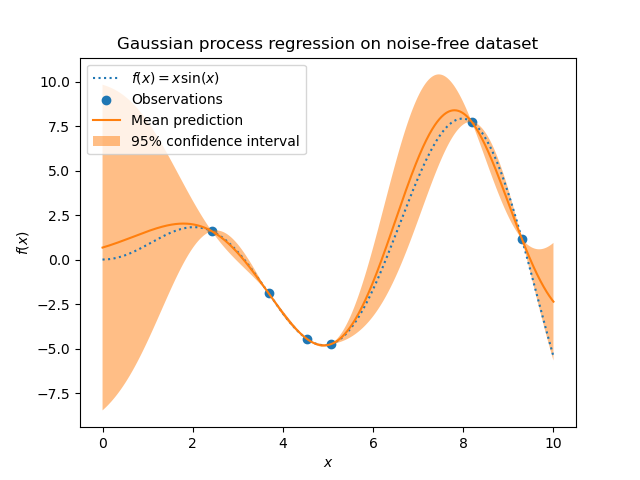
Un autre exemple : A priori, les réseaux de neurones sont aussi puissants que les processus gaussiens. En revanche, ils ont une tendance à avoir besoin de beaucoup d’information pour apprendre à prédire des nouvelles valeurs (d’où l’expression que pour du ML, il faut du Big Data). En même temps, pour fonctionner sur petits échantillons de données, vous pouvez utiliser les processus gaussiens et « encoder » dans la définition de processus ce que vous connaissez concernant le problème (votre à priori : périodicité, forme, etc). Dans ce cas, le processus gaussien sera plus performant que le réseau de neurones sans contredire le théorème.

(Image : SciKit, Processus Gaussiens, Interpolation par 20 points).

Autrement dit, NFL ne dit pas qu’il faut arrêter de chercher les meilleurs approches (un théorème n’est pas défaitiste) – il dit que la comparaison « synthétique » d’algorithmes n’a pas de sens – c’est toujours en appliquant l’algorithme aux données qu’on saura s’il fonctionne bien ou non. En même temps, NFL propose choisir un « à priori » et l’utiliser dans la construction de votre modèle ! (Car sans cet à priori tous les algorithmes sont les mêmes).

Conclusion : le futur ne se trouve pas que dans le Big Data, mais surtout dans les algorithmes adaptés à la réalité autour de nous.

Bonne santé à vous et à vos modèles.