Cet article est la suite de notre série concernant la consolidation de données. Aujourd’hui, nous allons parler de rapprochement (identification de doublons, record linkage).
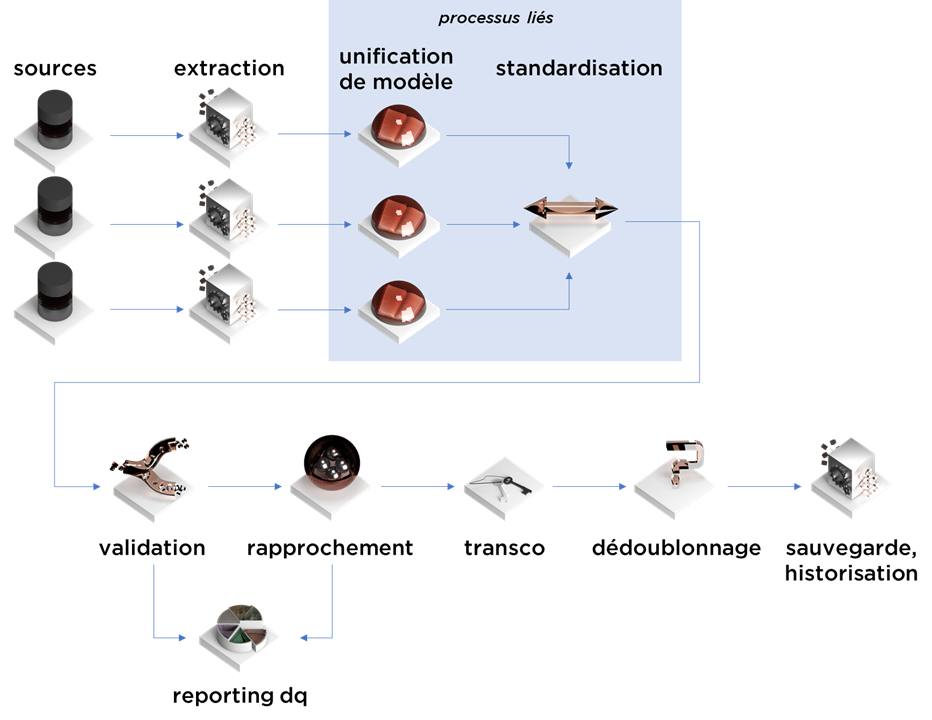
Nous avions déjà évoqué le sujet il y a quelques temps (https://ithealth.io/rapprochement-de-donnees/, https://ithealth.io/dont-do-it-la-cle-fonctionnelle-business-key/), mais aujourd’hui, nous allons faire une révision des méthodes existantes tout en analysant comment le rapprochement s’intègre dans le processus de consolidation.
Quel est l’intérêt ?
Toute consolidation de données doit répondre à la problématique des données dupliquées : les clients / fournisseurs / collaborateurs / factures / contrats / obligations / etc peuvent exister simultanément dans plusieurs SI voir en double dans le même SI.
Il faut avoir à l’esprit que ce n’est toujours pas la faute du ou des systèmes – les processus fonctionnels peuvent exiger une telle duplication (ex. un système opérationnel de transport peut demander la re-saisie du point de destination dans le cas où le contact est amené à changer – un tel processus est plus simple à implémenter que les autres alternatives). Par contre, pour obtenir une vision consolidée des données, nous pouvons être intéressés par une vision plus « globale », plus « propre ». Il nous faut donc extraire les entités uniques depuis les données dupliquées.
Avant d’obtenir la vision centralisée, nous devons identifier les répétitions (« doublons » dans un certain sens) en utilisant la « nouvelle » définition que nous venons d’établir avec notre modèle unifié de données.
I.e. à cette étape, nous voulons regrouper les « doublons » ensemble, par exemple avec un ID unique :
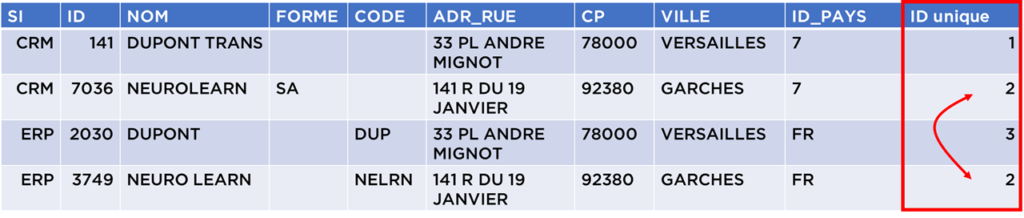
Note : nous voulons un identifiant plus « stable » possible, i.e. d’une exécution à l’autre il doit rester le même si possible.
Préparation : encore de la data governance
Dans notre exemple, lors de l’étape de mapping vers le modèle unifié, nous avons obtenu un modèle qui représente les objets suivants :
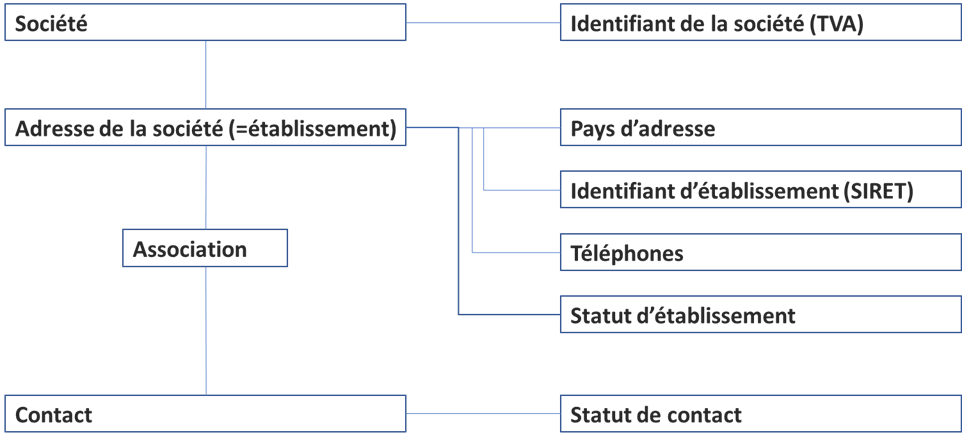
Pourtant, on se rappellera que dans les données de départ, les notions de société et d’établissement n’existaient pas :
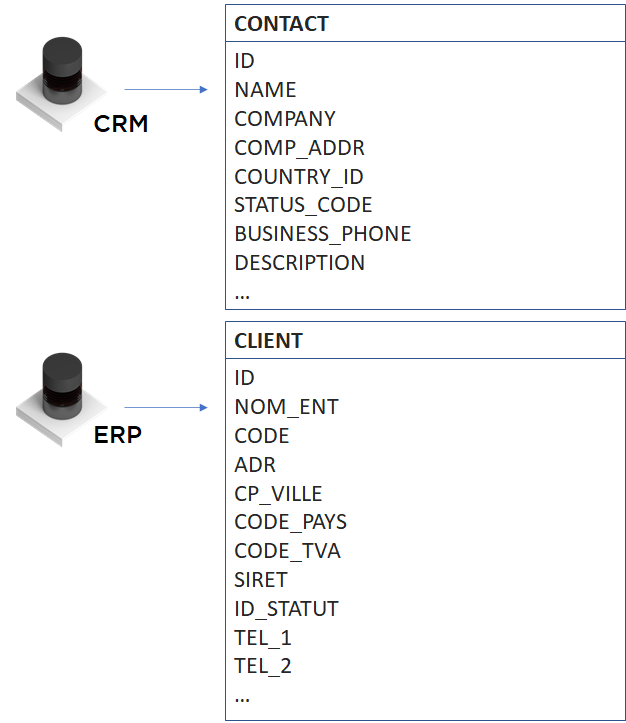
Ainsi, notre première tâche c’est de donner une définition la plus exacte possible aux nouveaux objets et en général c’est tout sauf facile (https://ithealth.io/difficulte-de-definir-dictionnaire-data-governance-mythique/, https://ithealth.io/data-governance-dictionary-histoire-dune-definition/), mais dans notre cas nous pouvons commencer par les définitions suivantes :
- « société – organisation avec un code TVA unique » ;
- « établissement – société à l’adresse physique » (en France, à une même adresse, une société peut avoir plusieurs établissements juridiques avec des codes SIRET différents. Nous pouvons faire une exception pour les établissements français : « sauf si nous connaissons les codes SIRET et qu’ils sont différents ») ;
- etc.
Maintenant, nous devons prévoir tous les cas que nous pouvons rencontrer avec les données. Supposons que nous trouvons deux objets dans notre table de données standardisées, comment décide-t-on si cette paire représente un doublon ou pas ?
Par exemple :
- pour les sociétés :
- si le nom et le code TVA sont les mêmes (à delta du nombre minimal de fautes de frappe) pour les deux enregistrements après la standardisation, nous les considérons comme doublons ;
- si le code TVA est manquant (ou incorrect) pour l’un des deux enregistrements et le nom est « assez complet », nous pouvons encore les considérer comme doublons ;
- si les noms sont assez proches, complets, mais avec des codes TVA différents – nous ne pouvons pas décider automatiquement – à revoir par les humains (Data Stewards) ;
- si les deux champs sont différents, alors ce sont des sociétés différentes sauf s’il existe des contre-indications (offrir la possibilité de forcer manuellement) ;
- etc…
- pour les établissements :
- si l’ID de la société est le même et les adresses sont proches, alors nous pouvons considérer les deux objets comme doublons ;
- etc…
Les méthodes
Vous avez du remarquer que nos définitions de « doublons » sont finalement assez floues, la cause à la :
- possibilité de fautes de saisie ;
- possibilité de rencontrer des données incomplètes ;
- possibilité qu’un objet a des représentations différentes que nous ne pouvons pas corriger avec la standardisation (ex. le même établissement au croisement de deux rues, pour ces deux entrées peut avoir deux adresses différentes) ;
- possibilité d’évolution des données (surtout pour les personnes physiques, i.e. contacts – changement de nom de famille, changement de poste, etc).
Il faut se faire une raison, il n’est pas possible d’identifier tous les doublons, mais nous allons faire de notre mieux.
L’algorithme le plus basique utilise une « clé fonctionnelle » (business key). Par exemple, pour une société, par définition le champ TVA (s’il est bien rempli) est une clé fonctionnelle – soit un identifiant unique. Autant s’en servir ! Il suffit d’associer avec chaque code TVA, un ID technique – et notre rapprochement est fini. Le problème majeur de cette approche, c’est notamment le cas où la qualité de cette clé (ou son taux de remplissage) n’est pas assurée. Plus de détail ici : https://ithealth.io/dont-do-it-la-cle-fonctionnelle-business-key/.
Les algorithmes plus avancés sont généralement construits en plusieurs étapes :
- indexation : pré-recherche de doublons potentiels avec un algorithme rapide ;
- pour les données trouvées dans un indexe – comparaison des champs de même nature pour estimer leurs proximité;
- scoring du résultat avec un modèle mathématique plus ou moins complexe pour identifier la proximité d’objets ;
- comparaison du score avec des seuils pour trier les données en :
- doublons ;
- non-doublons ;
- cas à revoir manuellement (d’où le besoin d’avoir des data stewards = humanware).
L’indexation
Durant le rapprochement, nous cherchons à identifier les paires de lignes qui correspondent à une certaine règle de gestion de « proximité ». Par contre, si nous traitons naïvement cette tâche, notre algorithme ne se finira jamais.
Par exemple, pour 1 000 lignes, nous avons 499 500 paires potentielles
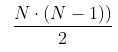
…mais il est clair que la vaste majorité de paires ne contiendra pas de doublons.
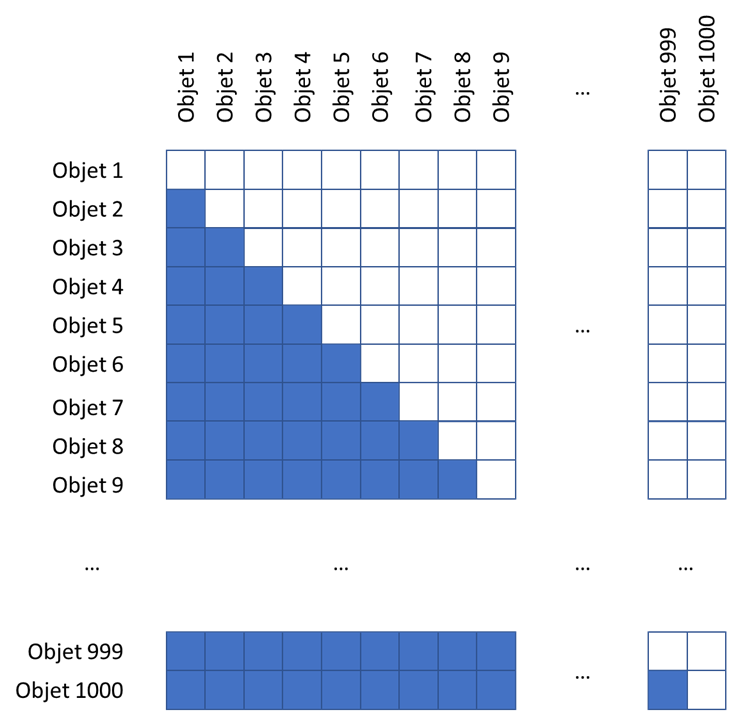
Le processus d’indexation doit nous permettre de réduire le nombre de comparaisons que nous allons exécuter dans le traitement, i.e. ce processus peut rendre les « faux doublons », mais il doit minimiser ce nombre pour obtenir la meilleure performance (en termes de temps de traitement). En même temps, il ne doit pas « perdre » beaucoup de doublons car tout ce qui ne sera pas trouvé à cette étape ne sera jamais détecté en tant que doublon (sauf en cas d’action manuelle).
Il y a deux approches qui sont fréquemment utilisées :
- blocking (division en petits « blocks », i.e. groupes de lignes semblables);
- bucketing (inverted index).
L’approche « blocking »
Si vous l’utilisez, vous devez choisir des champs avec des valeurs de préférence « sûres » et bien « distribuées » (i.e. assez rares). Ensuite, nous allons regrouper les objets en utilisant ces champs et comparer uniquement les données qui sont dans ce même groupe (contiennent exactement les mêmes valeurs dans les champs choisis).
Il est évident que vous allez devoir faire plusieurs itérations. Par exemple, si nous essayons de rapprocher les données suivantes, nous pouvons choisir deux étapes de blocking :
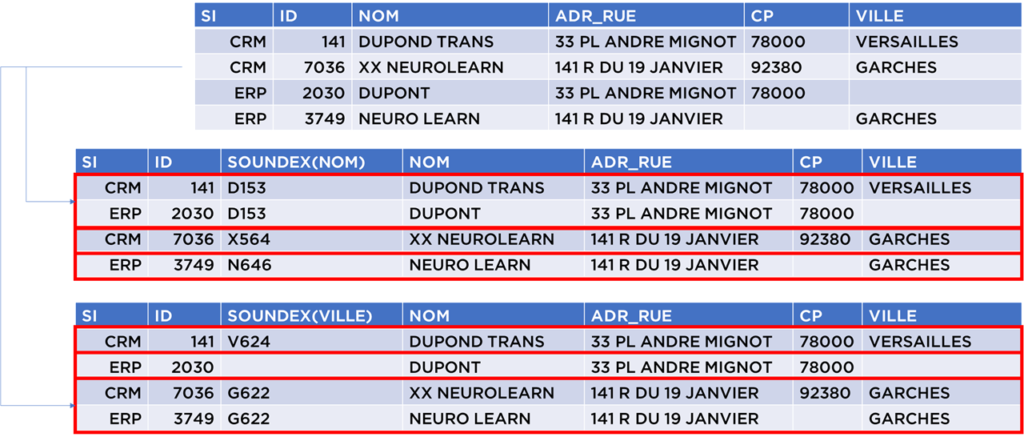
Vous pouvez voir qu’après deux étapes, les « doublons potentiels » se retrouvent ensemble au moins dans l’une de deux itérations.
À noter : L’approche « blocking » ressemble à l’algorithme de clé fonctionnelle. À la différence que la clé n’est pas obligatoirement unique. Nous avons le droit de faire plusieurs itérations avec des clés différentes car le résultat n’est pas considéré comme un doublon, mais plutôt comme un doublon potentiel.
L’approche « bucketing » (inverted index)
Dans l’exemple précédent, nous avons vu que l’approche de blocking fonctionne plutôt bien. Mais, il n’est pas très adapté aux valeurs textuelles qui bien souvent contiennent plusieurs mots et pour lesquelles l’ordre peut être inversé.
La solution c’est d’utiliser l’approche « bucketing » :
- nous allons prendre toutes données ;
- nous allons les diviser en « tokens » – c’est une expression qui énonce les mots ou combinaisons de mots ou mots transformées avec soundex ou une autre fonction ;
- pour chaque token on va identifier les objets où il est utilisé ;
- ensuite, pour chaque objet de notre table, nous pouvons chercher dans cet indexe tous les autres objets qui lui ressemblent.
Par exemple, pour les données utilisées depuis le début, nous pouvons obtenir le résultat suivant :
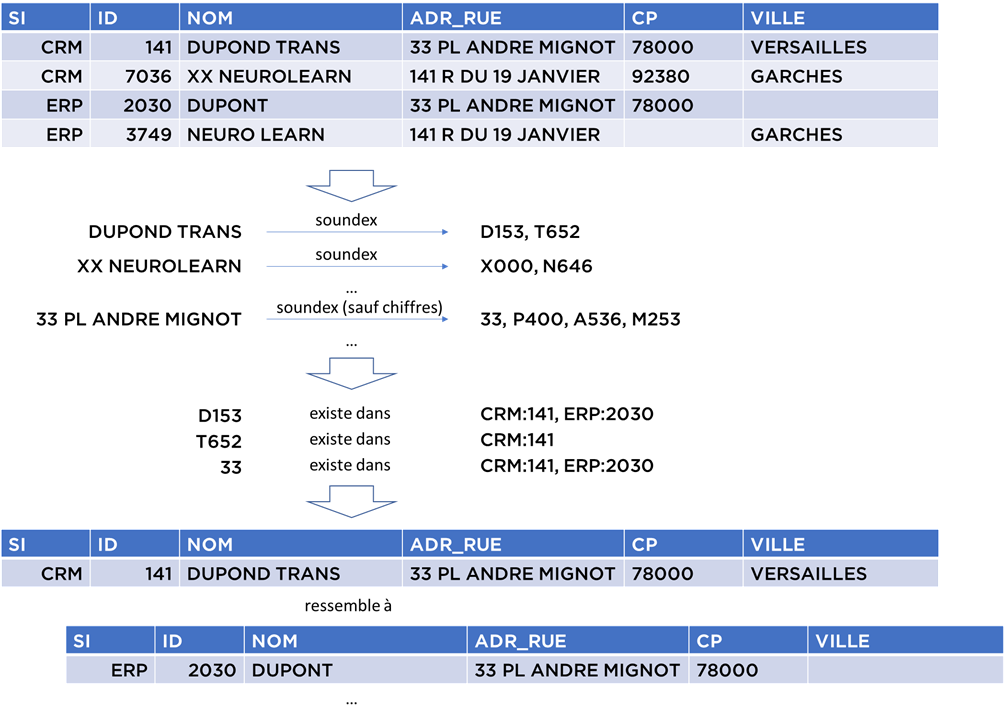
S’il existe au moins un mot (token) partagé par deux objets, la paire peut être trouvée en utilisant cette approche (contrairement au blocking qui est beaucoup plus « rigide »). C’est la force et la faiblesse de cette méthode car il y aura certainement des tokens fréquents : « PL », « RUE », « AV », etc – et nous essayons de garder le nombre de paires à la sortie de l’indexation la plus basse possible…
Il existe un nombre de techniques pour gérer ce problème :
- suppression de tokens trop fréquents ;
- pondération de tokens par la fréquence d’apparition (ex. algorithme TF-IDF) ;
- etc.
À noter : Cet indexe peut être rendu très performant en utilisant les hash tables et le tri des listes d’identifiants.
À noter : Pour les tokens nous pouvons aussi utiliser les parties des mots, par exemple les N-grams de caractères (souvent N=3 ou 4 caractères) qui sont les fenêtres glissantes de caractères consécutives.N-Grams-caractères("DUPONT", N=3) = liste("^^D", "^DU", "DUP", "UPO", "PON", "ONT", "NT$", "T$$")
Dans ce cas nous pouvons aussi tolérer les fautes de frappe dans chaque mot/code au niveau d’indexe.
La comparaison des champs
Une fois que nous avons obtenu les paires potentielles, nous devons comparer le contenu des champs pour pouvoir implémenter nos définitions « noms assez proches », « code TVA ne doit pas contenir trop de différences », etc.
Voici les techniques « standards » :
- comparaison de codes ou de texte court – décompte du nombre de caractères de différence : algorithmes de Levenshtein, Jaro-Winkler, Hamming, etc.
- comparaison de texte plus long : famille d’algorithmes TF-IDF (Soft-TF-IDF, BM25, etc), bi-tri-grams, etc ;
- comparaison de dates : variations de Levenshtein ;
- comparaison de montants : différence relative ;
- etc.
Voici un exemple :

À noter : Les modèles existants de comparaison sont imparfaits. Un jour, on reparlera de la « théorie PP » (qui est ordres de magnitude meilleure que l’état d’art et peut dépasser le niveau humain), mais pour l’instant, il faut se dire que même avec des réseaux de neurones, il est difficile d’obtenir des résultats bien meilleurs qu’avec des variations de Soft TF-IDF. Nous l’avons essayé !
Le scoring
Le scoring doit nous permettre évaluer le niveau de certitude que la paire d’objets représente bien un « doublon ». À cette étape, nous avons déjà calculé la « proximité » des champs.
Pour généraliser, nous pouvons dire que l’approche avec les clés fonctionnelles donne un score constant égal à 100% une fois les champs de a clé sont les mêmes (i.e. la paire identifiée au niveau de l’indexation).
Premièrement, il existe la méthode de Newcombe-Fellegi-Sunter qui est toujours considérée comme un état de l’art. Malgré sa forme, elle est très simple :
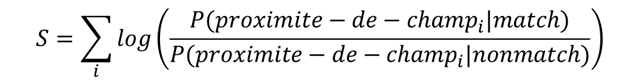
Il ne faut pas être intimidé par les probabilités. Voici ce que dit cette formule :
- si vous avez estimé la proximité des champs, il vous faut trouver un jeu de fonctions « d’activation » (fonctions croissantes) ;
- le résultat final sera une somme de ces fonctions appliquées aux proximités.
Autrement dit, nous pouvons oublier les probabilités et réécrire la formule comme une somme des fonctions croissantes 1D :
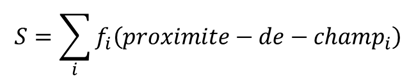
Toute la difficulté est dans la forme de ces fonctions. Il existe plusieurs techniques pour les estimer qui se basent soit sur des exemples préparés, soit utilisent la méthode d’espérance-maximisation (EM), soit supposent une certaine forme paramétrique des fonctions et permettent de saisir les paramètres.
Dans l’exemple ci-dessous, vous voyez l’interface de configuration de la forme pour l’un des champs dans IBM QualityStage. « m-prob » est « la probabilité d’obtenir les mêmes valeurs si les données sont en double », « u-prob » est « la probabilité d’obtenir les mêmes données par hasard » et Param1 – « proximité des champs quand le contenu deviens trop bruité ».
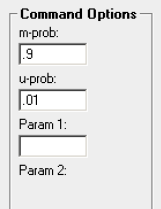
Dans notre exemple pour m-prob=0.9, u-prob=0.01 et Param1=750 (75%), la courbe donnera :
- si les champs contiennent les mêmes valeurs S = log₂(0.9/0.01) = 6.49 ;
- si les deux champs sont proches à 75%, S = 0 ;
- si l’un des deux champs est null, S=0 ;
- si les champs sont complètement différents : S = log₂((1-0.9)/(1-0.01)) = -3.31.
Certains éditeurs d’outils de Data Quality ignorent cette théorie et proposent le score à la base d’une somme pondérée (vous pouvez voir que la somme pondérée c’est un cas spécial de la théorie de N-F-S, où les fonctions sont linéaires). Dans ce cas, vous avez un paramètre de moins, voir un exemple d’Informatica Data Quality :

À noter : Le résultat d’une telle simplification est que votre scoring aura une qualité inférieure en comparaison avec les techniques plus avancées.
À noter : Le score peut être représenté sur différentes échelles équivalentes :
| Echelle | Valeur |
|---|---|
| Modèle de Newcombe-Fellegi-Sunter en log₂ | X |
| Modèle de Newcombe-Fellegi-Sunter en log₁₀ (en bels) | X/log₂(10) |
| Modèle de Newcombe-Fellegi-Sunter en 10*log₁₀ (en décibels) | 10*X/log₂(10) |
| Modèle de Newcombe-Fellegi-Sunter en forme de probabilité | sigmoid(X*ln(2)+const) |
Quand Fellegi et Sunter ont établi ce modèle (que nous considérons aujourd’hui comme l’état d’art), ils ont pris quelques raccourcis, notamment ils ont supposé que les valeurs dans les champs et les erreurs dans les champs sont indépendants. Il est vrai que cela fonctionne dans la plupart des cas, en revanche, parfois, nous avons besoin d’algorithmes plus avancés.
Pourquoi ? Voici une interprétation graphique.
Si dans nos objets, nous avons que deux champs que nous comparons et nous avons trouvé les « proximités » x et y de ces deux champs pour une paire d’objets, nous pouvons évaluer que notre score aura la forme suivante (une couleur plus claire correspond à un score plus élevé) :
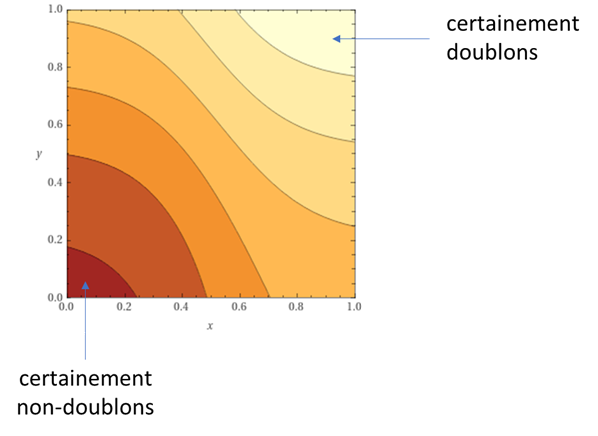
Supposons que nous testons notre modèle sur de nombreux exemples et nous trouvons que la forme de score doit être différente :
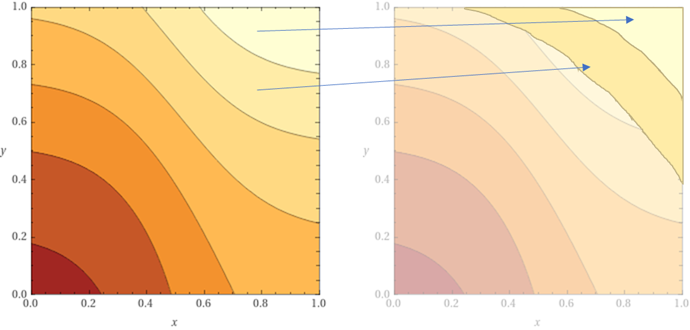
Malgré la forme erronée, nous pouvons toujours approcher certaines parties de ce modèle « parfait » avec notre modèle « imparfait ». Tout bon jusqu’au moment où nous rencontrerons les cas qui tombent pile entre les différents niveaux. I.e. même les modèles simples (ou relativement simples) fonctionnent tant que les données contiennent peu de différences (ou bien comme certains disent : avec des données de « bonne qualité »).
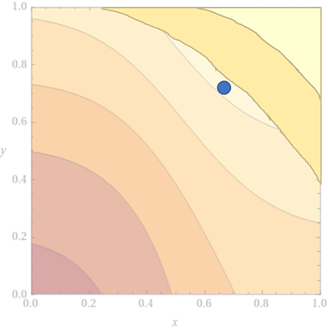
Aujourd’hui, vous avez certains éditeurs qui proposent des systèmes basés sur du Machine Learning. Certes, ils peuvent potentiellement prendre en compte plus de cas que la méthode de Newcombe-Fellegi-Sunter à la condition toutefois qu’il existe suffisamment d’exemples de données en entrée de l’algorithme, mais cela reste un cas particulier.
Vu que nos méthodes (autres que PP :)) sont imparfaites, souvent les éditeurs proposent un « false positive filter » (FPF).
Par exemple, si vous tolérez un certain nombre d’erreurs dans les prénoms des personnes et que vous rencontrez les jumeaux Adrien et Adrienne, nés le même jour, qui habitent ensemble… vous allez très certainement les considérer comme des doublons (une seule personne).
Pour ce cas, certaines solutions prévoient une technique de diminution de score pour certaines situations particulières (un filtre), ex. « prénoms proches, mais différents, noms de famille mêmes, date de naissance – même, sexe différent, alors diminuer le score à 70% ».
La prise de décision
Une fois nous avons nos scores, nous devons estimer deux seuils :
- seuil de rapprochement automatique,
- seuil de non-rapprochement,
…pour diviser les « doublons potentiels » (paires de données) en trois catégories :
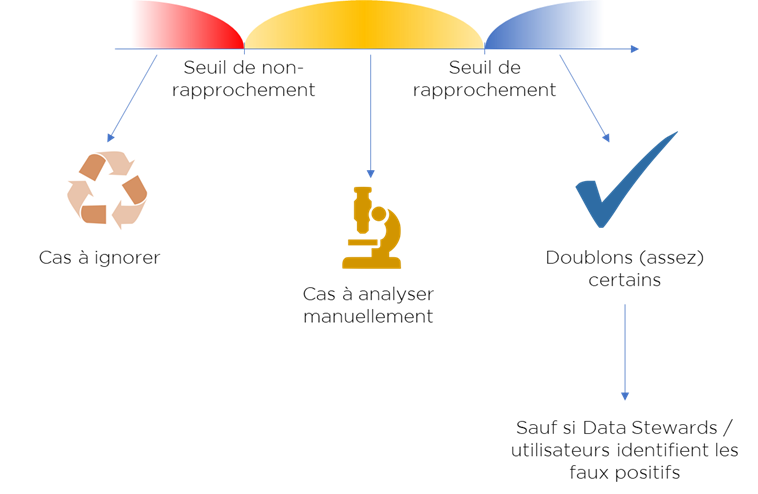
Nous considérons comme doublons uniquement les paires avec un score qui dépasse le seuil de rapprochement automatique. Les données avec un score inférieur à celui-ci et supérieur au seuil de non-rapprochement sont les cas à revoir manuellement (clericals, Data Stewardhip tasks). Les autres cas sont ignorés.
De plus, nous devons laisser à nos utilisateurs la révision des faux positifs dans le cas de rapprochement automatique. La logique semble très complexe mais fort heureusement, il existe l’approche qui permet de gérer ces cas.
Nous allons créer une nouvelle table que nous allons appeler « tâches », où nous allons garder tous les cas revus et à revoir :
- identifiants d’objets ;
- (option) score (en décibels ou probabilité) ;
- statut :
- à revoir,
- revu en tant que non-doublon,
- revu en tant que doublon,
- (option) revu comme un cas impossible à résoudre;
Tous les cas « à analyser » seront disponibles dans cette structure, mais en plus, on pourra y mettre tous les « faux positifs », i.e. tous les cas identifiés automatiquement comme doublons, alors qu’ils ne le sont pas :
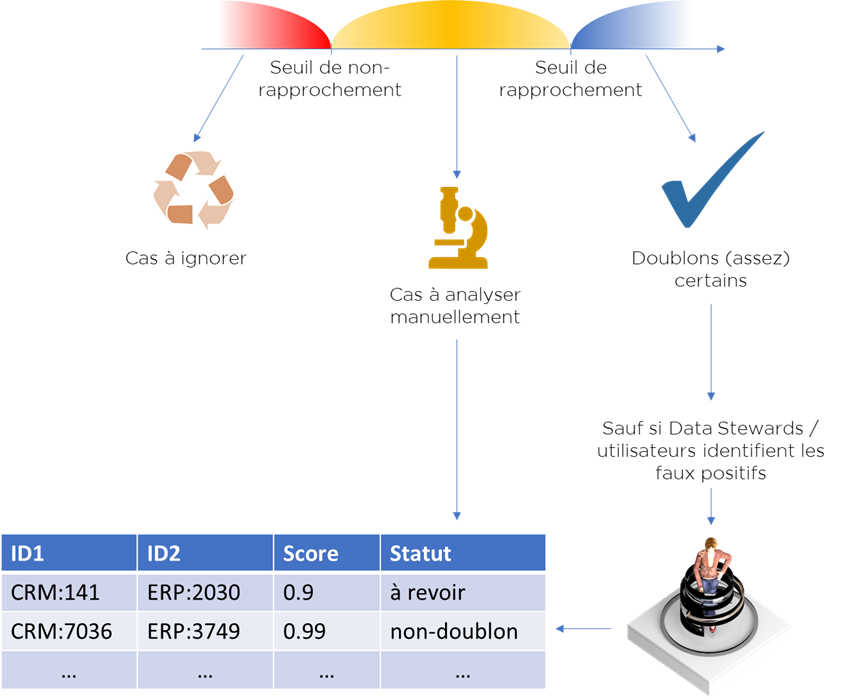
Cette « table » peut être utilisée par l’algorithme pour « forcer » les décisions, i.e. par exemple même si le score est très haut mais que la décision humaine est « non-doublon », l’algorithme va bien considérer la paire comme un « non-doublon ».
Conclusion : Si vous faites correctement le rapprochement, vous devez avoir une interface pour vos Data Stewards afin de gerer cette table des tâches.
Question restante : comment définir les seuils…
Techniquement quand vous rapprochez les données, il y a deux risques possibles :
- vous ne trouvez pas un doublon existant (« faux négatif ») ;
- vous identifiez à tort deux objets différents comme un seul et même objet, donc un doublon (« faux positif »).
Si nous utilisons qu’un seul seuil, les résultats d’algorithme peuvent être présentés sous la forme d’une courbe qui représente la qualité d’algorithme et l’état des données :
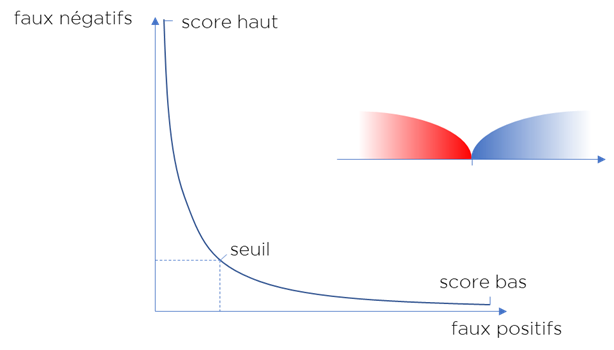
Vous pouvez changer le seuil, mais vous allez perdre soit au niveau d’un paramètre, soit au niveau d’un autre…
Pour améliorer l’algorithme, nous utilisons deux seuils, mais au prix du salaire des data stewards :
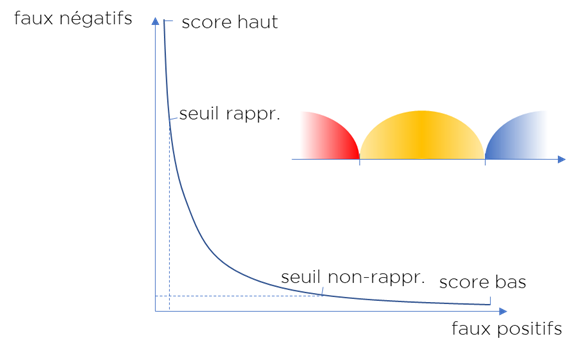
Conclusion : nous devons trouver le juste milieu entre le nombre de faux positifs, le nombre de faux négatifs et la quantité des cas revus manuellement.
Dans le monde idéal :
- on calcule :
- les risques liés aux faux positifs ;
- les risques liés aux faux négatifs ;
- le prix à payer pour la résolution de chaque tâche ;
- on estime le coût total en fonction de deux seuils ;
- on l’optimise (i.e. on trouve les deux seuils qui minimisent le coût total).
Dans le monde réel, on utilise la métrique « WTF » :
- on itère :
- on ajuste les seuils ;
- on montre les résultats aux utilisateurs ;
- on écoute l’impression.. et on s’arrête au moment où les utilisateurs sont contents des résultats.

La génération d’IDs
N’oublions pas notre but : la génération de clés uniques pour nos tables de transcodification…
Une fois que nous avons trouvé pour tous nos objets les doublons, nous obtenons un graph comme celui-ci (chaque point – objet de la table source, chaque lien – paire de « doublons identifiés ») :
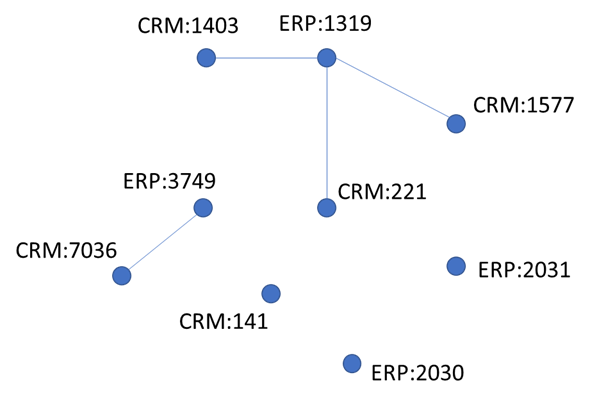
Maintenant à chaque partie connexe de graph nous devons assigner un identifiant – ça sera la valeur à mettre dans notre table de transcodification.
L’une des techniques consiste à assigner l’identifiant unique à chaque objet de graph :
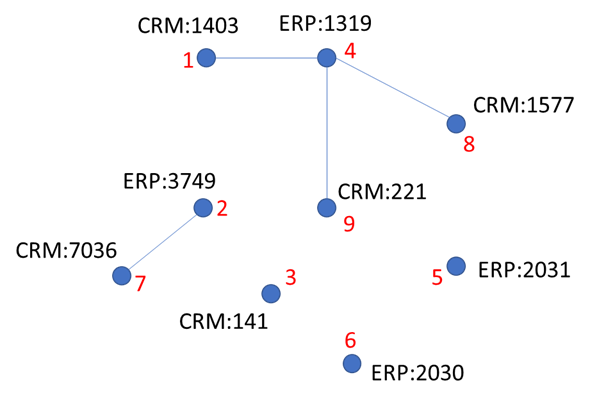
Ensuite avec un algorithme itératif, on trouve l’ID minimal dans chaque partie connexe :
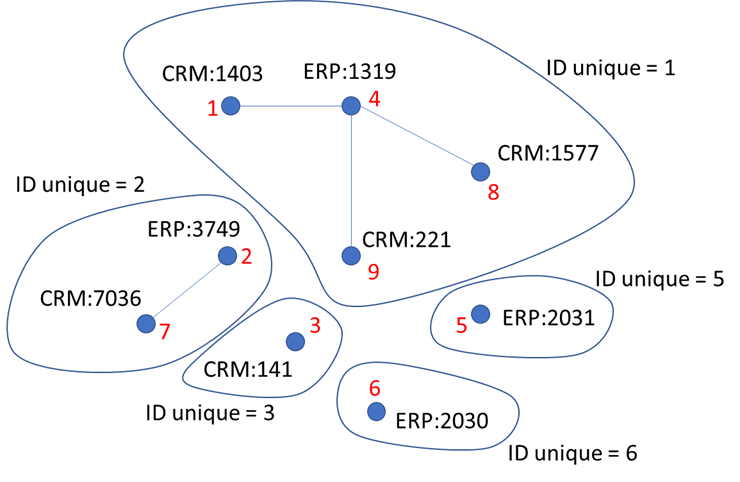
Puis, nous pouvons enfin générer la table de transcodification :
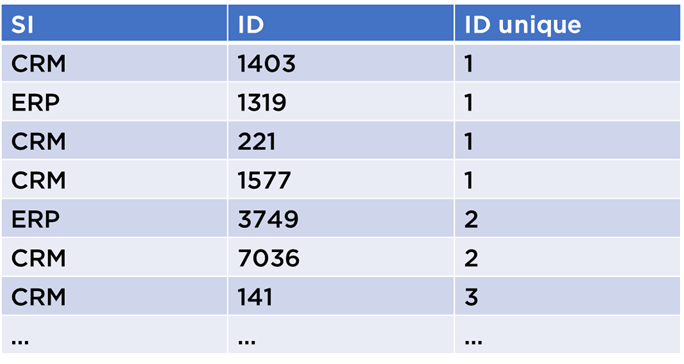
Pour rendre l’algorithme « stable », i.e. pour qu’il donne les mêmes identifiants d’une exécution à l’autre, il suffit d’associer les IDs aux lignes qu’une seule fois et sauvegarder cette association. Nous avons le droit de recalculer le graph à chaque exécution et si les données ne se changent pas, nous allons toujours recevoir la même table de transcodification.
Recapitulatif
Les outils de rapprochement peuvent utiliser des approches très différentes en donnant des résultats de qualité variable :
| Méthode | Comparaison des champs | Indexation | Scoring |
|---|---|---|---|
| Clé fonctionnelle | Egalité | Blocking | 100% (néant) |
| Rapprochement basique | Floue / Permissive | Blocking | Linéaire |
| Newcombe-Fellegi-Sunter | Floue / Permissive | Blocking | Somme de fonctions non-linéaires |
| Newcombe-Fellegi-Sunter | Floue / Permissive | Bucketing | Somme de fonctions non-linéaires |
| ML | Floue / Permissive | Blocking ou Bucketing | Réseaux de neurones, arbres de décision, etc |
Aussi, les approches varient d’un éditeur à l’autre :
| Méthode | Comparaison des champs | Indexation | Solutions |
|---|---|---|---|
| Clé fonctionnelle | Egalité | Blocking | Fait maison |
| Rapprochement basique | Floue / Permissive | Blocking | Talend, Informatica Data Quality, Semarchy, EBX, etc |
| Newcombe-Fellegi-Sunter | Floue / Permissive | Blocking | IBM QualityStage |
| Newcombe-Fellegi-Sunter | Floue / Permissive | Bucketing | IBM MDM Standard Edition |
| ML | Floue / Permissive | Blocking ou Bucketing | Solutions peu connues |
Enfin, dans la majorité des outils, il manque l’UI de data stewardship pour la gestion des tâches (donc à vous de l’ajouter) :
| UI | Solutions |
|---|---|
| Non | Talend, …, QualityStage, … |
| Partiel | Informatica Data Quality, … |
| Oui | IBM MDM Standard Edition, … |
C’est pour ça que si vous choisissez un outil pour votre projet de consolidation, vous devez estimer le niveau de qualité de résultat attendu et vos capacités pour ajouter des modules manquants.
Conclusion
Le rapprochement est le cœur de la consolidation. Il est très important d’être bien équipé pour obtenir des résultats fiables à cette étape.
J’espère que cette révision rapide de ce domaine vous permettra de mieux choisir (ou développer) une solution de rapprochement.
Bonne santé à vous et à vos systèmes.

