– Nos Data Scientists ont analysé les données et découvert que la quantité vendue ne dépend pas du prix de vente. Du coup, votre solution n’a aucune utilité pour nous.
– Mettez donc votre prix à l’infini. Ainsi, vous obtiendrez une marge infinie.
Echange avec une société
Aujourd’hui nous vous proposons un sujet difficile, mais qui nous concerne certainement tous. Notre article peut être utile aux décideurs, mais il est également intéressant comme use case pour les Data Scientists. Le sujet que nous allons aborder, c’est également un problème moral, même si nous ne considérerons pas cet aspect aujourd’hui.
Problème
Chaque société (sauf à but non-lucrative comme une association) a pour objectif de produire un revenu pour ses collaborateurs et ses dirigeants / actionnaires. Pour permettre l’analyse, prenons le schéma suivant (très simplifié):
- flux d’argent (cash in) de clients qui achètent des produits permet à la société d’exister,
- …mais une partie de cette argent est utilisée pour payer les impôts, etc,
- …une partie reste bloquée dans le stock,
- …et une partie (cash out) est payée aux fournisseurs.
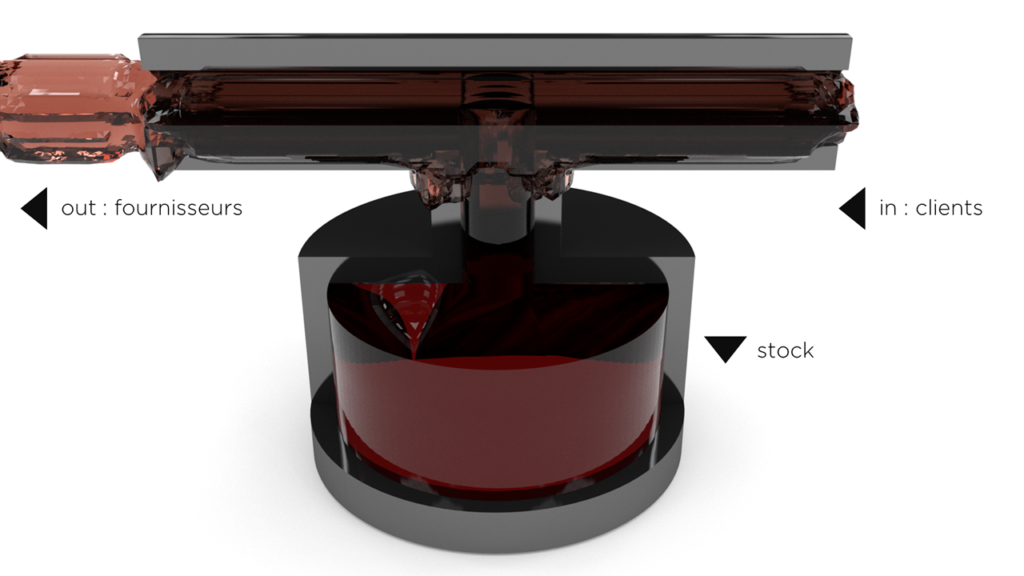
Quand une société optimise ses revenus, elle peut corriger chaque partie de ce flux et obtenir les meilleures bénéfices possible à court ou à long terme.
Nous allons nous concentrer aujourd’hui sur l’optimisation du flux entrant (cash in), et plus précisément sur un levier important – le prix des produits.
Méthodes
Il existe de nombreuses approches différentes à l’optimisation des prix suivant la nature du produit que vous vendez :
- vous vendez un produit unique (ex. fréquence 5G, art) – la vente aux enchères est une solution optimale, l’automatisation n’existe pas, mais il existe des modèles mathématiques extraordinaires basés sur la théorie des jeux pour identifier le prix de base (et c’est important);
- vous vendez un produit en mode B2B donc vous êtes obligés de conduire des négociations, donc la compétence du négociateur est le facteur clé;
- vous vendez un produit taillé en fonction du client (ex. assurance) – optimisation possible, automatisable, mais complexe;
- vous vendez les produits en quantités importantes avec un prix fixé (ex. grande surface, certains produits bancaires).
Nous nous concentrons sur le dernier sujet dans cet article car dans les autres cas les autres facteurs peuvent être plus importants que le prix, ex. compétences du vendeur. De plus, sous certaines conditions, les solutions « à prix fixé » peuvent également s’appliquer aux produits « taillés aux clients », donc notre article peut être également intéressant pour les assureurs, par exemple.
Méthode #0. Prix de vente = coût de revient + marge
Cette approche classique a servi durant des centaines d’années aux marchands de toutes sortes. L’idée c’est de mesurer quelle marge nous voulons et nous pouvons avoir pour chaque groupe de produits (ex. 15% pour les matières de construction ou 70% pour les produits alimentaires).

Le reste vous pouvez le calculer dans un fichier Excel – vous devez calculer le prix qui vous fera 0 marge (coût de revient) en ajoutant au prix d’achat le prix de transport, de stockage, etc, puis le chiffre obtenu est multiplié par le coefficient de votre choix.
Une solution facile, mais nous pouvons voir tout de suite qu’elle n’est pas complète car tout problème est dans votre choix du coefficient – si il est trop bas, vous auriez pu faire plus de marge, si il est trop haut – vous aurez peu de clients. Comment définir le coefficient ?
Méthode #1. S’aligner sur la concurrence
Le problème du coefficient de marge semble impossible à résoudre… mais nous avons une économie assez ouverte, où le marché est roi, n’est-ce pas ? La solution serait donc de regarder le prix de vente des concurrents et de s’aligner par rapport au marché ?
Pourquoi nous pouvons le faire maintenant et comment faire ?
Aujourd’hui la grande majorité des produits est disponible via Internet, il suffit d’aller chercher dans Google le site de notre concurrent et il est fort probable que nous y retrouverons ses prix. Cela s’appelle « web scrapping » et c’est tellement courant que vous avez même le choix de récupérer les données par vous-même via Java/Python ou d’utiliser les services de sociétés spécialisées (IBM, PriceEDGE et centaines d’autres). Vous avez même des outils de protection de votre site contre le scrapping !
Qu’allez-vous trouver si vous cherchez les données de la concurrence ?
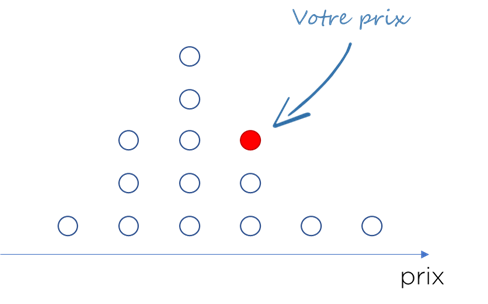
Vous aurez la visibilité sur vos concurrents et la distribution des prix. Il est fort probable que votre prix n’est ni le plus bas ni le plus haut. Veut-il dire qu’il est optimal et qu’il ne faut rien faire ?
Certes, nous avons obtenu plus d’information, mais notre approche semble imparfaite. Oui, vous pouvez toujours dire « et maintenant tout dépend de votre stratégie ». Est-ce vraiment la solution ? En effet, je peux formuler une stratégie comme « maximiser le chiffre d’affaire à la condition que la marge moyenne ne soit pas inférieure à 15% », mais comment puis-je implémenter cette stratégie avec les données à ma disposition ?
Réponse : je ne peux pas… (même si les éditeurs vont essayer de vous prouver le contraire en vous montrant de belles interfaces…)
Une autre question qui peut traverser l’esprit des décideurs « mais ma brand a de la valeur, donc je peux mettre mon prix au dessus de mes concurrents ». Comment estimer le rôle de votre brand / de la présentation / etc ?
Méthode #2. Élasticité
L’approche un peu plus scientifique c’est de se dire qu’il existe une dépendance entre le prix que nous avons fixé et la quantité de produits vendus. Cette dépendance est connue sous le nom de « courbe de la demande ».
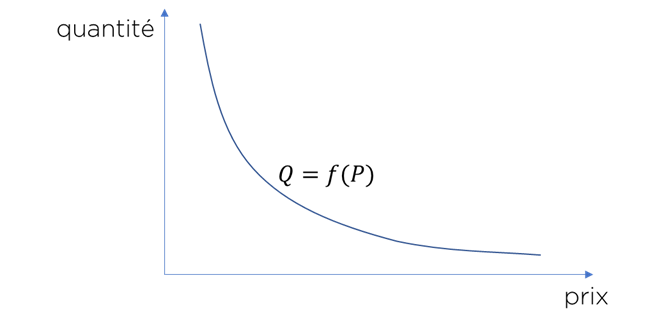
Les économistes ont l’habitude de décrire cette courbe avec un coefficient d’élasticité, qui est défini comme un ratio de vitesse relative du changement de la quantité vendue à la vitesse relative du changement de prix :
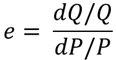
Wow ! Les formules, les mathématiques ! Vous pouvez même calculer le revenu marginal en utilisant l’élasticité, donc si vous supposez que l’élasticité est constante, vous pouvez calculer le prix optimal !
Sauf que… l’élasticité n’est pas constante ! Nous n’avons pas appris grand chose. Avec le même résultat, nous avons pu supposer que la courbe de la demande est linéaire.
Note. L’auteur a lu des publications « scientifiques » qui supposent que la courbe de la demande est linéaire… donc les ventes deviennent négatives avec des prix élevés.
Méthode #3. Machine learning
Nous « savons » qu’il existe une courbe de la demande. Si nous pouvons « apprendre » cette courbe, nous pouvons également apprendre à extrapoler notre revenu.
Effectivement, il existe 2 types de résultat que nous pouvons maximiser : chiffre d’affaire et la marge, mais les deux dépendent de la quantité vendue et du prix de revient seulement :
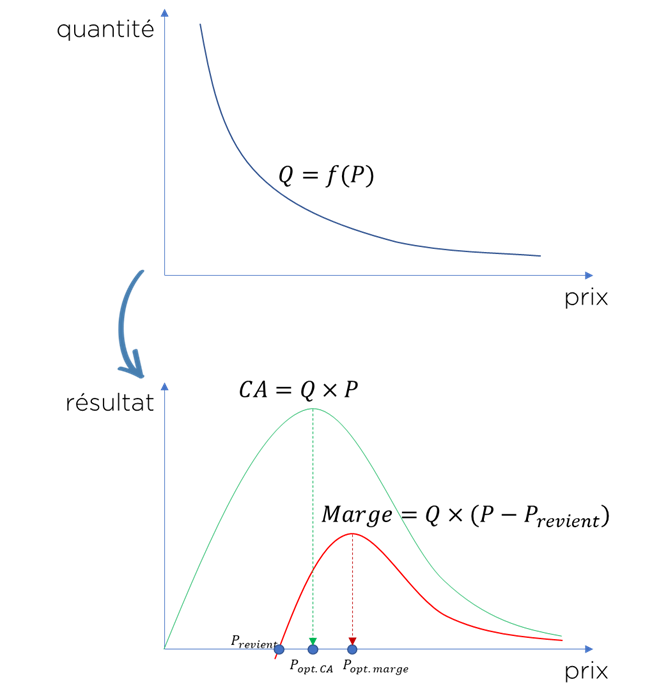
Si nous pouvons estimer la courbe de la demande à partir de nos données de vente, nous pouvons automatiquement prendre en compte le comportement des clients vis-à-vis de notre brand et beaucoup d’autres paramètres. Faisons payer les clients ce qu’ils sont prêts à payer ! Cela s’appelle Value Based Pricing, i.e. que le client paye autant qu’il valorise notre produit, pas autant que le produit coûte en production.
Prenons les réseaux de neurones et… ça ne marche pas bien (voire pas du tout).
Pourquoi exactement ? La raison est simple : vous pouvez varier le prix qu’un nombre de fois fixe. De plus, le bruit (marge d’erreur) dans les données sera importante. Si on résume, vous aurez peu de données et un bruit important, donc le résultat sera certainement médiocre… Moment de tristesse et de solitude…
Méthode #4. Modèle statistique de base
Prenons notre temps pour analyser la situation :
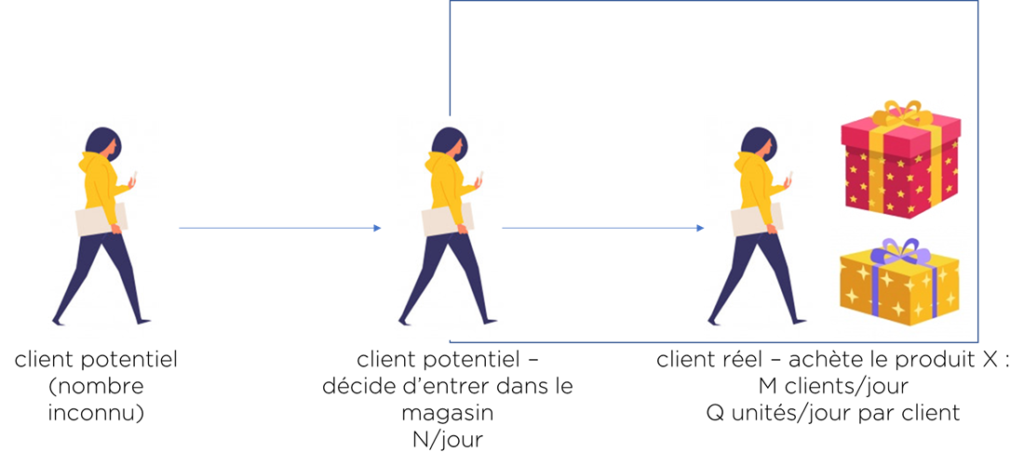
- il existe un nombre de personnes qui sont nos « clients potentiels » – le nombre est souvent inconnu, mais il peut être amélioré via publicité/marketing/etc – ce n’est pas notre sujet, c’est du marketing;
- si le client montre de l’intérêt (décide d’entrer dans le magasin ou sur notre site) – nous pouvons le compter comme un vrai client;
- si le client achète le produit X (il existe une facture), nous connaissons, combien de personnes ont acheté ce produit et en quelle quantité.
Dans ce processus il y a deux choix importants qui nous intéressent :
- la personne décide d’acheter ou pas – probabilité d’achat,
- la personne décide d’acheter, pour quelle quantité achetée – distribution de probabilité d’achat de Q unités.
En fait, notre courbe de la demande se divise en deux car si on change le prix, nous pouvons avoir plus/moins de personnes qui achètent le produit en question (pourcentage d’acheteurs) ou les acheteurs peuvent décider de consommer plus/moins de produit en question (quantité moyenne de vente). Du coup, une courbe de la demande n’a pas beaucoup de sens… et le bruit que nous avons observé est très important car c’est une « multiplication » de deux bruits différents (aucun des deux n’est Gaussien).
Pour les Data Scientists. Les bruits ne sont pas du tout Gaussiens car : (1) les deux valeurs sont positives (ou zéro), (2) la variation de l’un dépend de l’autre, (3) la distribution de la quantité achetée aura une forme différente entre les produits rarement vendues et les produits fréquemment vendues (notamment il n’est pas possible de vendre peu de produit fréquemment vendu, alors qu’avec les produits rarement vendus cette condition ne fonctionne pas).
Ce moment quand tu comprends que la microéconomie ne fonctionne pas (il n’y a pas d’une courbe de la demande, mais il existe au moins ces 2 composants) :

Il nous reste juste à comprendre la forme de ces deux composants de la fonction de demande…
Nous pouvons supposer que :
- il existe une zone de « peur » quand le prix est trop bas. En effet, nous ne voulons pas acheter le produit car nous considérons qu’il n’est pas possible d’avoir un bon produit pour ce prix;
- il existe une zone de prix trop bas pour que nous le prenons en considération (pas de problème pour acheter le produit pour ce prix);
- il existe une zone de « bifurcation » où les clients potentiels commencent à se poser la question s’ils veulent vraiment le produit à ce prix;
- il existe une zone « trop cher » pour la majorité des clients potentiels;
- la zone de « peur » est rarement utile dans une vraie optimisation, donc nous pouvons l’ignorer;
- la courbe pour la quantité de produits peut avoir la même forme que la courbe pour le pourcentage d’acheteurs.
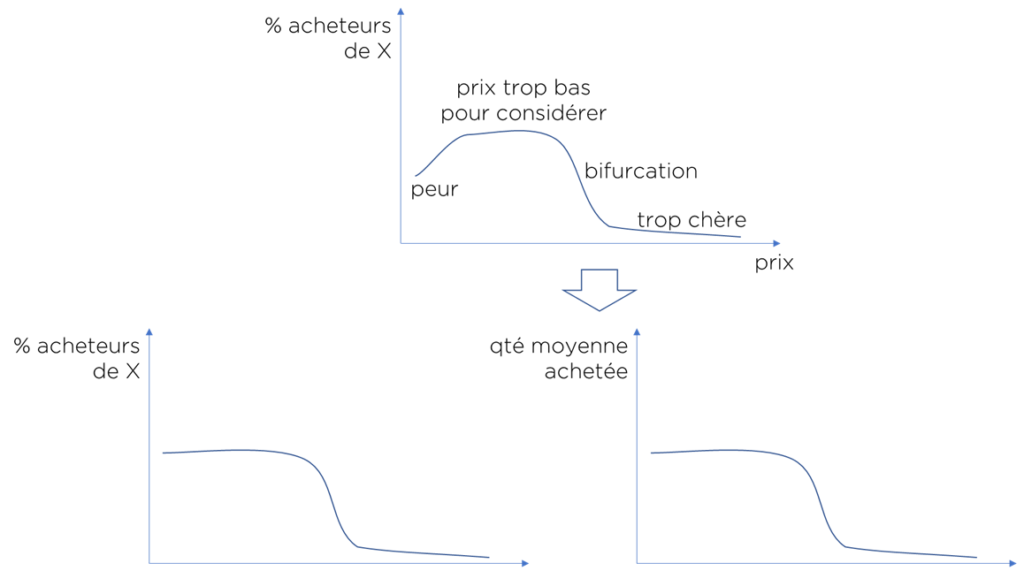
Note concernant le client au début d’article… La manque de dépendance entre la quantité vendue et le prix veut dire que le prix est sur l’un des deux plateaux : « prix trop bas » ou « prix trop élevé »… évidemment.
Maintenant nous pouvons supposer une forme paramétrique de ces courbes (si vous cherchez, vous allez trouver plusieurs dizaines de publications avec différentes suppositions non-linéaires!). Dans notre cas, nous pouvons prendre une sigmoïde (car elle fonctionne mieux que certaines autres courbes)… mais encore une fois c’est une faiblesse de notre approche car personne ne connaît la vraie forme des courbes… et un mauvais choix impactera la qualité de l’algorithme et, avec, les résultats financiers de la société.
En quelques jours/semaines/mois, il est possible de constituer un modèle statistique qui pourra trouver les paramètre des courbes (surtout si vous prenez en compte les changements dans le temps : les trends et la saisonnalité).
Si vous utilisez MCMC, par exemple (https://ithealth.io/hacking-et-magie-la-programmation-statistique-cest-cool/), vous allez pouvoir estimer les distributions de probabilité des paramètres de votre modèle et donc la distribution de probabilité des prédictions (c’est important car en plus à l’estimation de prix optimal vous voulez connaître votre incertitude) :
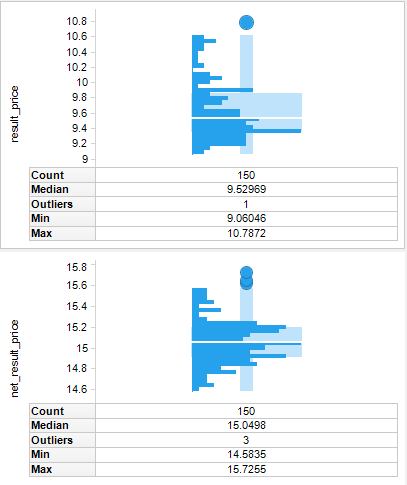
Ci-joint, vous pouvez voir deux distributions des prix optimisés : pour le CA (en haut) et pour la marge (en bas). Il existe une incertitude d’estimation des paramètres car la quantité d’information est très limitée, mais au moins, nous avons une visibilité !
Dans ce cas, par exemple, le prix optimal pour le CA est approximativement entre 9,2 et 9,8; pour la marge – entre 14,8 et 15,3…
À noter que nous avons pris beaucoup d’hypothèses, notre algorithme (MCMC) est super-méga-lent, ceci étant dit, néanmoins, nous avons des résultats plus ou moins compréhensibles. En plus, nous avons « gratuitement » les trends de la perception du prix :
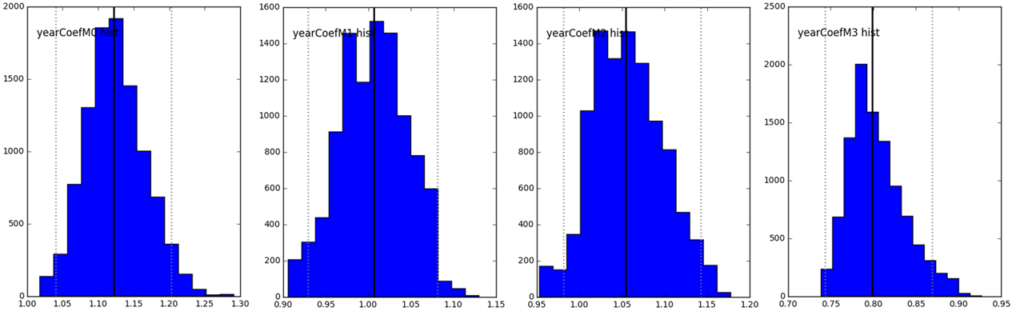
Au dessus, vous voyez le coefficient devant les paramètres des sigmoïdes sur l’axe de prix pour 4 ans, puis d’une année à l’autre il se diminue (en moyenne) et plus en plus vite. Cela signifie que les clients veulent payer moins pour ce même produit. Faut-il chercher à mettre à jour la liste des produits vendus ?
Note. Notre modèle montre que la diminution de la demande n’est pas forcement liée au fait que les prix sont trop élevés, ce sont probablement juste les clients qui sont partis en vacances… ou ce n’est pas la saison pour le produit en question (courbes de la demande bougent « en bas », pas « à gauche ») donc il n’y a pas toujours de sens à diminuer le prix… et vous n’imaginez pas un instant combien de managers baissent les prix sans analyser la cause… Pour vraiment détecter la cause d’un changement de comportement, il faut faire varier les prix et utiliser un algorithme car visuellement ces deux cas sont impossibles à distinguer.
Méthode #5. Optimisation Bayésienne
Les hypothèses sur la forme des courbes ? Une heure de calcul ? Plusieurs mois ou d’années d’historique ? Est-ce que cette solution sera viable pour les nouveaux produits ?
Nous avons fait une bonne analyse de processus, des distributions de probabilité (non-Gaussiennes), mais notre algorithme (MCMC) et nos hypothèses concernant les courbes « % acheteurs » et « quantité moyenne » sont probablement à remplacer…
Pour que vous compreniez mieux la profondeur du problème, voici une petite visualisation :
- souvent on modifie le prix une fois par jour,
- …donc nous avons une seule observation de nombre d’acheteurs et de la quantité vendue pour un prix donné par jour,
- …mais les courbes de la demande (inconnues si nous ne prenons pas d’hypothèses) bougent d’une journée à l’autre suivant les trends du marché,
- …donc ce que nous voulons c’est trouver la surface d’évolution du marché par une courbe des points observés (bruités)…
- …et puis trouver la cross-section de cette surface pour le dernier moment t (temps)…
- …et la courbe obtenue peut être utilisée pour calculer le CA, la marge et les optimiser.
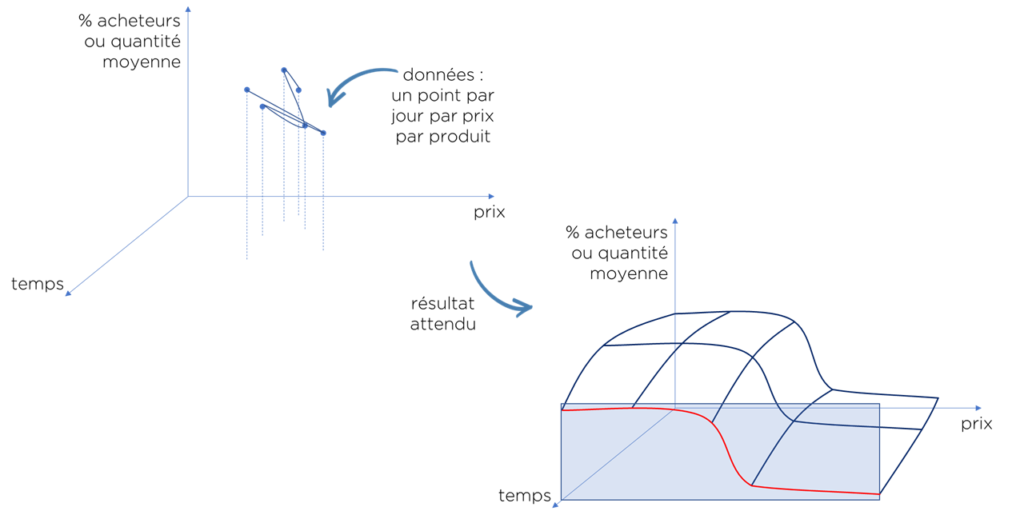
Si vous avez compris la suite des réflexions, vous devez vous dire que c’est impossible ! Surtout, si vous ne connaissez ni la forme des fonctions de la demande (cross-section X-Y), ni la vitesse du changement du marché (forme de cross-sections X-Z, Y-Z) – les inputs de notre MCMC. Est-ce que nous pouvons lever ces hypothèses ?
Il existe un super-héros qui peut nous sauver la mise : l’optimisation Bayésienne.
Les méthodes d’optimisation Bayésienne sont conçues pour optimiser les fonctions inconnues, sans connaître les dérivées (ni probablement les valeurs exactes – à cause de bruit) en faisant un minimum de pas.
Au niveau superficiel, voici ce qui se passe :
- …nous allons tester quelques prix pour avoir un premier input à l’algorithme,
- …nous allons donner une estimation des fonctions de la demande avec les processus Gaussiens (même si l’erreur n’est pas Gaussienne),
- …nous allons concevoir un algorithme qui maximise la probabilité de trouver le prix optimal le plus vite possible et nous allons appliquer cet algorithme, obtenir le prix et le tester dans notre magasin / agence,
- …réitérer.
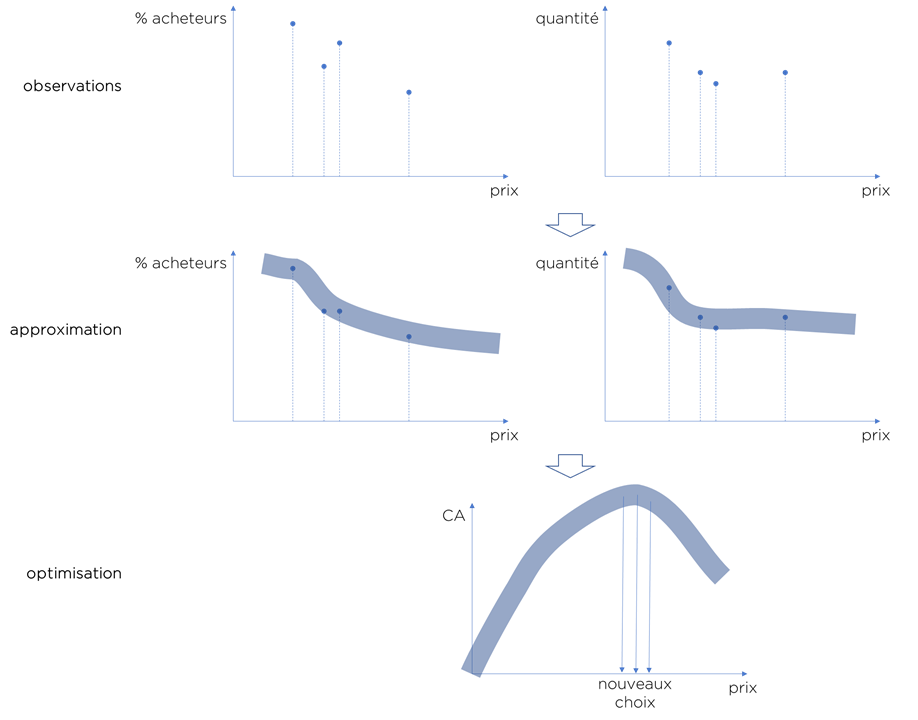
Vu que l’algorithme trouve l’optimum très vite, nous pouvons ignorer les trends du marché (ou nous pouvons les prendre en compte dans un algorithme plus avancé).
Le vrai problème ici est dans le choix de bon processus Gaussien et du bon algorithme de recherche des prix à essayer (qui ne doit pas seulement trouver le prix optimal, mais aussi permettre d’apprendre le plus vite possible des courbes de la demande). Si les choix ne sont pas optimaux, la vitesse d’optimisation peut être d’ordres de magnitude plus lente.
Voici un exemple de fonctionnement d’algorithme de ce type (Azeria) sur les données synthétiques (la courbe grise – premier input, orange – optimisation, bleu – observations bruitées, rose – optimum) : en 10-15 itérations (jours) l’algorithme trouve l’optimum (+6% de revenu) et continue de l’explorer par la suite.
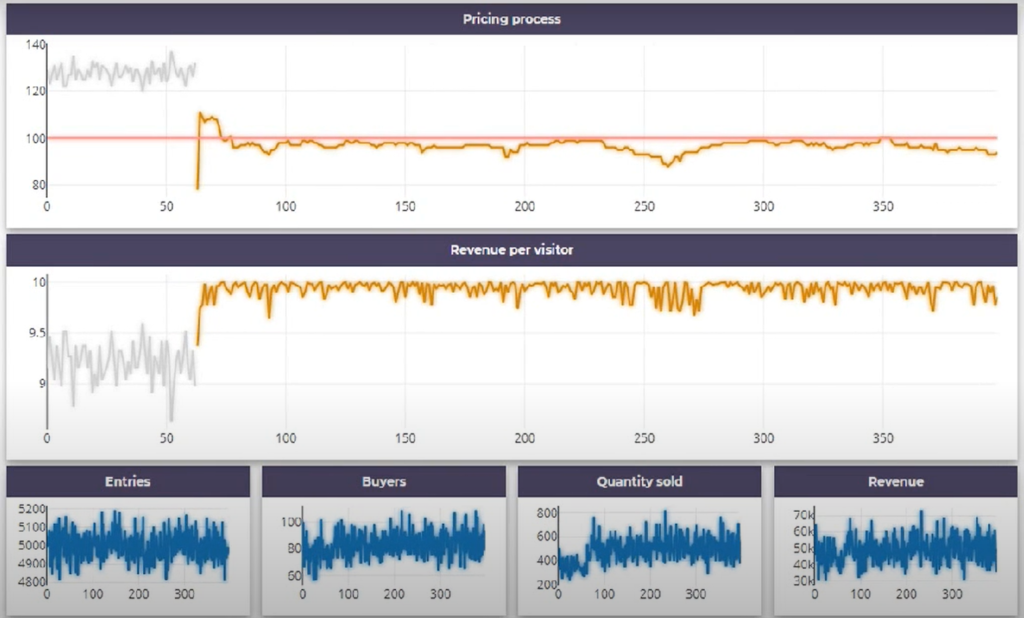
…et encore, nous n’avons pas abordé le sujet de l’interdépendance entre les produits (ex. substitution), les événements exceptionnels, les soldes, etc.
Conclusion
Un sujet aussi important que la gestion des prix est souvent sous-estimé. Dans le monde du Big Data, on pense que tout problème de ce type est déjà résolu et n’a aucun intérêt scientifique, mais fort heureusement, ce n’est pas encore le cas. En plus à « Big Data », il y a des problèmes de « Small Data » qui nécessitent de nouvelles approches mathématiques.
Bonne santé à vous et à vos sociétés.

