Rasez-vous régulièrement avec le rasoir d’Occam

Aujourd’hui, je voudrais aborder avec vous un outil assez intéressant et à mon avis, très important. Vous pourriez penser que notre sujet est philosophique, mais pourtant, il a des conséquences très concrètes sur les modèles mathématiques, l’IA, etc.

Occam

Notre histoire démarre par un théologien, philosophe et logicien anglais ayant vécu au XIII-XIV siècles, William (Guillaume) d’Occam (Ockham). Fortement décrié en son temps pour ses travaux novateurs, soupçonné même d’hérésie, il est connu pour ses apports dans de nombreux domaines : physique, politique, logique. Mais aujourd’hui, penchons nous sur son apport en épistémologie, i.e. la théorie de la connaissance.

L’expression la plus connue qui nous est parvenu, employée sous le nom de « rasoir d’Occam », est la suivante :

Les multiples ne doivent pas être utilisés sans nécessité

I.e. si nous pouvons expliquer les observations avec une théorie simple plutôt qu’avec une théorie complexe, nous devons prioriser la théorie la plus simple. En effet, Occam suivait la logique de ses prédécesseurs, par exemple, celle d’Aristote :

C’est en vain que l’on fait avec plusieurs ce que l’on peut faire avec un petit nombre

Très bien, mais… admettons que nos amis philosophes se trompent ? Et si ce postulat ne fonctionne pas ? Eh bien, dans ce cas, nous pourrions procéder à l’invention de théories aussi complexes et aussi absurdes que nous voulons, par exemple :

…entre la Terre et Mars se trouve une théière de porcelaine en orbite elliptique autour du Soleil, personne ne serait capable de prouver le contraire pour peu que j’ai pris la précaution de préciser que la théière est trop petite pour être détectée par nos plus puissants télescopes. Mais si j’affirmais que, comme ma proposition ne peut être réfutée, il n’est pas tolérable pour la raison humaine d’en douter, on me considérerait aussitôt comme un illuminé…

Théière de Russell

De même manière fonctionnent les religions de Licorne rose invisible (https://fr.wikipedia.org/wiki/Licorne_rose_invisible) et de Pastafarisme (https://fr.wikipedia.org/wiki/Pastafarisme).

Dit autrement, si nous ne croyons pas dans le rasoir d’Occam, nous vivons dans un monde que nous ne pouvons pas « apprendre et comprendre » et cela signifie que la science ne peut pas exister… Cela contrarie fortement nos « desiderata »…

Le problème avec la philosophie, c’est qu’il est difficile de mesurer ces « multiples » pour vérifier et prouver qu’une théorie est plus complexe (donc moins probable) que l’autre…

Gödel

Notre histoire reprend par le rêve des mathématiciens et par la personne qui l’avait détruit.

Faisons un saut temporel au début du XX siècle. Après (ou plutôt en fin de) la révolution industrielle, beaucoup de mathématiciens furent inspirés par l’idée de la codification et de la formalisation (mécanisation) des mathématiques. L’idée était de décrire les mathématiques avec un langage universel suffisamment détaché de l’interprétation possible. Dans ce cas, réfléchissait les formalistes, le reste peut être obtenu via un calcul mécanique qui se basera sur les règles prédéfinies.

Hélas, en 1931, un mathématicien autrichien, Kurt Gödel, qui avait encore 25 ans a publié ses fameux théorèmes d’incomplétude.

L’idée de ses deux théorèmes est la suivante : si vous avez un langage assez puissant pour décrire une certaine théorie (l’arithmétique, par exemple), vous pouvez également l’employer pour construire des expressions qui ne peuvent pas être ni prouvées ni réfutées.

Cela signifie que pour prendre la décision concernant ces nouvelles expressions, il vous faudra « compléter » la théorie avec le nouveau postulat, mais même dans ce cas, la théorie ne sera jamais complète.

L’autre résultat incroyable est que même dans notre petit monde mathématique, construit par nous-même, la tâche de recherche de nouveaux postulats est tout sauf simple… en fait, elle ne peut pas être accomplie avec les moyens de notre théorie, ni avec aucune autre tactique formelle, i.e. nos théories ne sont pas complètes, mais de plus elles ne sont pas faciles à compléter.

En disant cela avec les mots de XXI siècle, même la théorie mathématique ne peut jamais être complétée par un ordinateur, peu importe sa puissance.

Note. L’idée centrale des théorèmes est que si notre langage est assez puissant, nous pouvons avec ce langage décrire les raisonnements concernant lui-même (comme une analyse introspective). Il se trouve que pour répondre aux questions de ce type, il faut toujours avoir des concepts d’un niveau supérieur.

Turing

En 1936, Alan Turing, mathématicien, philosophe, cryptanalyste, etc travaille sur une reformulation des théorèmes de Gödel.

Pour analyser ce problème, il propose un modèle d’un ordinateur universel – la machine de Turing. La machine a une forme d’un ruban (potentiellement de longueur infini) et une tête qui peut se déplacer tout au long du ruban, lire et modifier les chiffres sur le ruban suivant quelques règles prédéfinies.

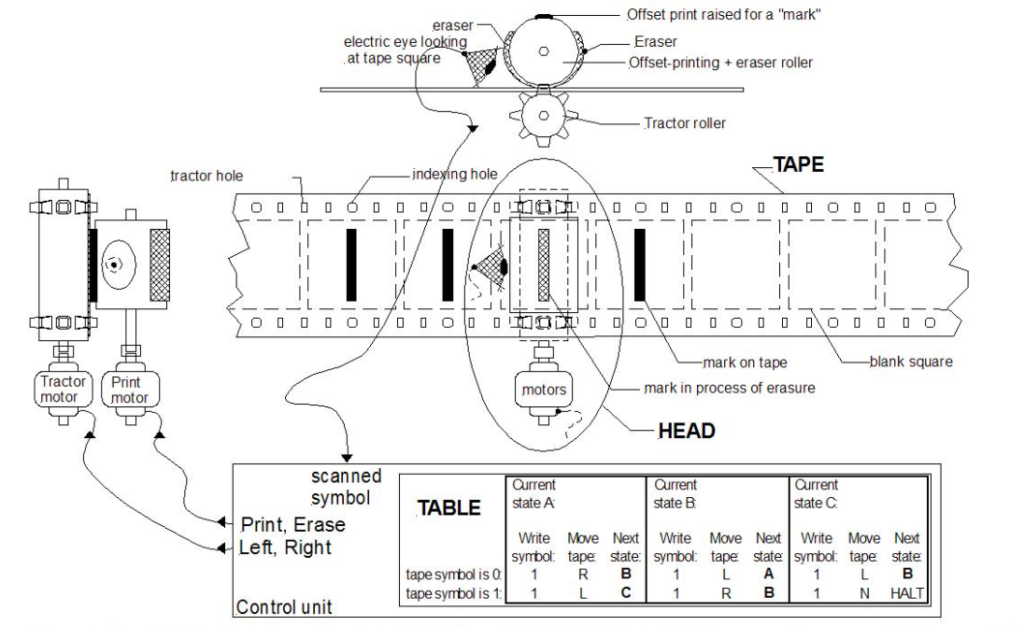
Malgré l’apparence simpliste, cette machine est en capacité d’accomplir tout algorithme imaginable.

Turing prouve les postulats suivants :

• la machine est vraiment universelle, i.e. elle peut accomplir tout algorithme,
• …mais elle-même ne peut pas faire la rétrospection de ses propres programmes, par exemple, pour décider si le programme s’arrêtera ou fera un boucle infini (problème d’arrêt),
• …puis Turing prouve le théorème de Gödel en démontrant qu’il est équivalent au problème d’arrêt, qui ne peut pas être analysé avec cette machine.

Autrement dit, la machine de Turing, équivalente à tout autre ordinateur, peut accomplir tout algorithme, mais il existe des problèmes qui ne peuvent pas être décrit sous forme d’algorithmes.

Solomonoff et Kolmogorov

Plus tard, dans les années 1950 et 1960, Ray Solomonoff et Andrey Kolmogorov arrivent indépendamment à une nouvelle définition qui sera plus tard baptisée « complexité de Kolmogorov » malgré le fait que Solomonoff était un peu en avance avec sa théorie de la « probabilité algorithmique ».

L’idée est que si une théorie prédictive peut être décrite en forme d’algorithme (de la façon la plus courte possible), la probabilité de la théorie se diminue exponentiellement avec la longueur de programme qui l’implémente (pour une certaine machine de Turing).

Cela crée une incertitude : les différentes versions de machines de Turing peuvent donner des longueurs différents de programme, mais il a été prouvé que malgré les différences d’architecture, la différence de longueur de programme ne sera pas si importante…

Le seul problème c’est avec la formulation de l’algorithme « plus court possible ». Malheureusement, il a été également prouvé qu’il n’y a aucun algorithme qui peut trouver la description « plus courte possible » d’algorithme.

Autrement dit, si vous avez deux théories qui décrivent les mêmes observations et si vous pouvez convertir les deux en algorithmes, il est facile de choisir la meilleure théorie – c’est celle qui se convertie en algorithme plus court… par contre, vous n’avez aucun moyen pour prouver que votre implémentation est vraiment la plus courte possible.

Vous avez probablement remarqué que cette nouvelle théorie répète le postulat d’Occam, mais cette fois en forme probabiliste et plus constructive. Si on pouvait automatiquement « optimiser » les algorithmes pour les « compresser », on aurait pu créer une machine qui de façon optimale aurait pu analyser les différentes explications aux différents évènements et finalement étudier le monde autour de nous. Le seul problème est qu’un tel machine ne peut pas se baser sur une architecture d’un ordinateur (machine de Turing).

Encore un rêve

Nous vivons dans un monde où les réseaux de neurones attirent (encore) beaucoup d’attention. Beaucoup de sociétés investissent dans l’Intelligence Artificielle…

Ce mouvement existe aujourd’hui en partie à cause de fait que certains pays (Canada, Etats Unis, par exemple) n’ont jamais abandonné la recherche dans ce domaine, même durant « l’hiver de l’IA ». L’un des chercheurs et les influenceurs les plus connus est Geoff Hinton.

Voici ce qu’il dit à MIT Technology Review :

Je crois vraiment que le deep learning sera capable de tout faire, mais il nous faudra un nombre de découvertes conceptuelles…

https://www.technologyreview.com/2020/11/03/1011616/ai-godfather-geoffrey-hinton-deep-learning-will-do-everything/

A noter. Cela peut ne pas être clair, mais tout « deep learning » peut être exécuté sur une « machine de Turing » (ce que nous faisons déjà), donc il ne peut pas être « plus puissant » que la machine de Turing.

Conclusion

Le rasoir d’Occam est un outil très important car sans cet outil la science est impossible. Assez étonnement, nous l’employons presque quotidiennement pour prendre des décisions, alors qu’il est prouvé qu’il n’existe aucun algorithme pour le faire. Alors, l’intelligence est-elle vraiment algorithmisable ?

Bonne santé à vous et à vos systèmes !