Tous. Nous avons tous pris des cours de probabilité au collège, au lycée ou bien à l’université. La probabilité est une notion fondamentale qui nous impacte de différentes manières suivant les circonstances : à titre d’exemple, nous avons tous en tête la déclaration le 24 janvier dernier, à la sortie d’un conseil des ministres, de l’ancienne ministre de la santé Agnès Buzyn, sur le risque de propagation du Covid-19 en France.

« […] le risque d’importation d’importations de cas depuis Wuhan […] il est maintenant quasi nul […] les risques de propagation du coronavirus sont très faibles […] ».

Dans cette déclaration, Mme Buzyn évoque la notion de risque qu’on peut définir par la définition suivante : la possibilité de survenue d’un événement indésirable, la probabilité d’occurrence d’un péril probable ou d’un aléa ». Partant de cet exemple pour le moins parlant, dans l’article ci-dessous, nous allons aborder l’interprétation des probabilités, en vous présentant certaines notions qui lui sont associées. Soyez rassurez, il ne s’agit pas d’un article à connotation politique, et les notions techniques évoquées sont abordables par tous.  

La Probabilité, de quoi s’agit-il réellement ?

Dans cet article, nous allons découvrir ensemble la notion de la probabilité. À travers l’histoire, l’Homme a expérimenté et amélioré des moyens pour mesurer des quantités physiques comme le temps ou la température. Chacune de ces quantités représente un aspect précis et bien défini de l’état du monde physique qui est par ailleurs informative, comme la température extérieure peut nous permettre de décider quel type de vêtements faut-il porter aujourd’hui.

La probabilité est une quantité décrivant la tendance physique qu’un événement se produise ou mesurant avec quelle force un événement peut se produire.

La probabilité est bien une quantité qui mesure quelque chose, elle dispose d’une définition mathématique précise et non ambiguë, en revanche, elle ne se rapporte pas au monde physique de manière aussi simple et intuitive que des mesures comme la longueur et la vitesse. 

La probabilité d’un évènement est un nombre réel compris entre 0 et 1, plus le nombre et grand ou proche de 1, plus il est plus probable à se produire, et plus est proche de zéro, moins il est probable à se réaliser. L’étude de la probabilité s’est largement démocratisée depuis le 18ième siècle avec l’étude des jeux de hasard et d’autres phénomènes imprévisibles représentant l’aspect aléatoire lié à des expériences ou certains phénomènes.

Il existe quatre interprétations concurrentes bien connues de la probabilité, chacune a une vision propre de la nature fondamentale de ce concept.

Toutes les interprétations de la probabilité en tant que notion respectent le formalisme mathématique basé sur des axiomes proposés par le mathématicien Andrey Kolmogorov, d’autre part, il existe un autre formalisme du concept de la probabilité proposé par le R.T Cox sous forme de théorème « Théorème Cox » qui permet de dériver les lois de probabilité à partir d’un ensemble de postulats. Bien avant, au début du 19ième siècle, le mathématicien Pierre-Simon Laplace a mis en place un système mathématique du raisonnement inductif basé sur les probabilités reconnues après par le bayésianisme qu’on aborderait dans d’autre article avec son « rival » le fréquentisme.

Andrey Kolmogorv à gauche, P-S Laplace à droite

La définition classique 

Les premiers essais pour définir la probabilité remonte au 19ième siècle. Connu de nos jours sous le nom de définition classique, elle se rapporte aux cas d’expériences aléatoires et bien définies. Selon cette définition, il faut diviser conceptuellement l’espace des possibilités en résultats probables, mutuellement exclusifs et collectivement exhaustifs. Ensuite, la probabilité d’un événement est définie comme le nombre de résultats favorables à l’événement, divisé par le nombre total de résultats possibles.

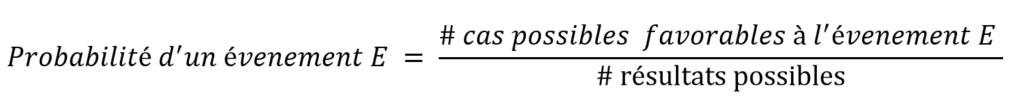
Prenons un exemple classique pour mieux illustrer cette définition, supposons que nous lançons un dé équitable (non biaisé) afin de calculer la probabilité de lancer un nombre impair.

Comme le dé est non biaisé, il est donc susceptible de se retrouver avec l’un de ses 6 côtés vers le haut. La répartition de l’espace des possibilités à ces 6 résultats satisfait l’exigence de la définition:

• Il couvre toutes les possibilités, en supposant que le dé ne peut pas rester stable sur un sommet.
• Tous les résultats (obtention d’un entier compris entre 1 et 6) sont probables.
• Les résultats sont mutuellement exclusifs (on ne peut pas obtenir deux nombres comme résultat à la fois pour un et seul lancement de dé).

Les résultats favorables à l’événement « obtenir un nombre impair suite au lancement du dé » sont 1, 3 et 5. Il s’agit de 3 des 6 résultats possible, donc la probabilité d’obtenir un nombre impair est de 3/6 (ou 0,5). Tout de même, il existe différentes façons de décomposer l’espace des possibilités, qui satisfont la définition.

Par exemple, au lieu de décomposer un jet de dé en 6 résultats possibles, on peut le décomposer comme suit:

• Nombre pair / impair
• Moins de 4 vs supérieur ou égal à 4
• En sous ensemble de l’espace de possibilité : {1, 2}, {3, 4}, {5, 6}

La granularité avec laquelle on décompose l’espace de possibilité dépend du type d’événement. La chose importante à considérer est de savoir si votre événement (et uniquement votre événement) peut être entièrement couvert par un sous-ensemble de votre espace de possibilité.

La première décomposition (impair vs. pair) fonctionnerait toujours pour calculer la probabilité de rouler un nombre impair. Mais les deux autres ne le seraient pas parce que les résultats possibles ne sont que partiellement cohérents avec l’événement.

Il existe un autre principe lié à cette définition qui nous a permis de calculer la probabilité d’obtenir un nombre impair dans l’exemple précédant. Ce principe postule que deux résultats devraient avoir la même probabilité s’ils sont symétriques par rapport aux facteurs qui les provoquent. Dans l’exemple de roulement du dé, les 6 résultats sont symétriques parce que la seule différence entre eux se trouve dans les étiquettes latérales n’ayant aucun impact sur le processus physique de l’expérience en question. De ce fait, tout argument qu’on peut considérer pour expliquer pourquoi un résultat particulier est plus probable que les autres peuvent également être utilisé pour l’un des autres résultats.

La définition classique n’est pas fausse. En fait, elle est tout à fait conforme à la définition mathématique, mais elle est limitée, l’espace de possibilité n’est défini que dans le cas fini. Selon cette définition, la probabilité d’un événement est égale à la fréquence à long terme de l’occurrence de l’événement lorsque le même processus est répété plusieurs fois.

La probabilité comme fréquence à long terme 

Selon cette définition, la probabilité de lancer un nombre impair est de 0,5 car le fait de rouler plusieurs fois la matrice conduit à environ la moitié des rouleaux qui sont impairs. Cette définition est différente de la définition du classique de deux manières principales:

• Elle ne fait pas référence au principe d’indifférence, les probabilités d’événements uniques ne sont pas déterminées à l’avance en analysant l’espace d’échantillonnage.
• Les probabilités ne peuvent être définies pour des essais uniques. Il s’agit d’une distinction très importante qui sépare cette définition des autres. Il n’y a aucune probabilité de lancer un nombre impair pour un unique lancement de dé.
• La probabilité est égale au pourcentage de résultats de « nombre impair » d’une série hypothétique de nombre infini de rouleaux.

En conséquence, la probabilité n’a de sens que dans des situations répétables. Par exemple si on souhaite prédire les élections présidentielles aux États-Unis sans considérer les candidats et en se basant sur l’historique des élections antérieurs serait une approche inappropriée. En effet, un président n’est pas choisi en réalisant une expérience de lancement de pièce de monnaie, le choix du président dépend des candidats et de l’humeur des électeurs qui change d’élection à élection.

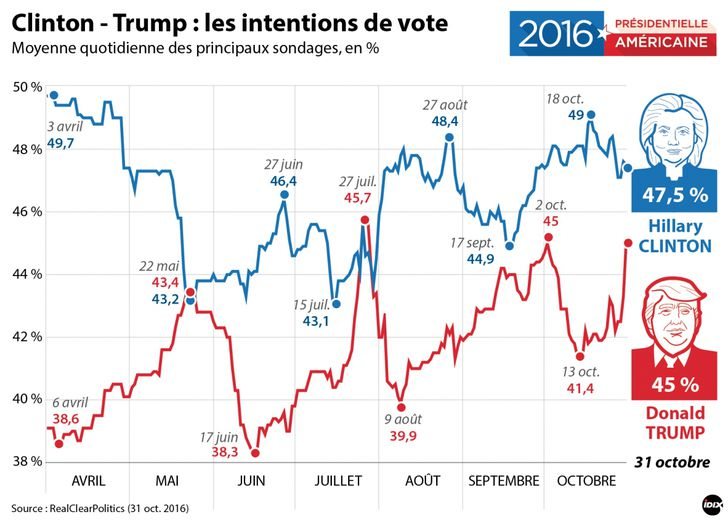
Avec cette définition, nous ne pouvons pas calculer les probabilités d’hypothèses. Chaque hypothèse est vraie ou fausse et les probabilités ne quantifient aucune incertitude. On peut nommer cette approche de fréquentiste car elle se base sur uniquement sur le fréquence d’événements. Nous avons toujours tendance à faire des affirmations de la sorte « il est peu probable que X soit vrai » (petit clin d’œil à notre désormais ex-ministre de la santé) ce qui implique que la probabilité que X soit vrai est faible. Or ces types de déclarations ne sont pas cohérentes avec cette conception fréquentiste de la probabilité ou la probabilité fréquentiste.

La loi des grands nombres 

Il existe une complémentarité à la définition fréquentiste de la probabilité. Elle s’appuie sur la loi des grands nombres. Cette loi est un théorème mathématique éprouvé qui relie les probabilités aux fréquences. La loi stipule qu’au fur et à mesure qu’on répète le même processus ou l’expérience (lancement d’une pièce de monnaie ou d’un dé), la fréquence relative d’occurrence d’un résultat particulier se rapprochera de plus en plus de la probabilité de ce résultat.

Par exemple, si on lance une pièce 10x, il est peu probable que vous obteniez 6 têtes, au lieu du « attendu » 5. Dans ce cas, la fréquence relative des têtes serait 7/10. Mais si on lance la même pièce 1000x, la fréquence relative des têtes sera beaucoup plus proche de 0,5 (489/1000 par exemple). La loi des grands nombres nous dit, qu’a force d’augmenter le nombre d‘expériences, la fréquence relative des têtes se rapprochera de plus en plus de 0,5.

La définition de la propension explique également le principe d’indifférence avec les propriétés physiques des objets. Par exemple, un dé n’est pas biaisé pour atterrir sur un côté particulier précisément parce que c’est un cube parfaitement symétrique, a une densité uniformément répartie. NB : Les deux interprétations précédentes ont une perception objective de la probabilité.

La probabilité comme une propension

Les interprétations de propension considèrent les probabilités comme des propriétés objectives d’entités dans le monde réel. La probabilité est considérée comme une propension physique, ou une disposition, ou une tendance d’un type donné de situation physique à produire un résultat d’un certain type, ou à produire une fréquence relative à long terme d’un tel résultat.

Par exemple, une pièce de monnaie peut atterrir sur pile ou face avec une propension de 0,5, cela n’est pas complètement vrai selon cette conception de probabilité : la pièce de monnaie fera plusieurs tours sur son tranchant avant de se mettre sur le côté pile ou le côté face. D’autre part, un dé a une propension de 1/6 à atterrir avec chaque côté tourné vers le haut, cette interprétation de la probabilité ne prête pas considération aux propriétés intrinsèques de l’objet étudié mais plutôt aux propriétés inhérentes de la situation dont l’objet fait partie.

Cette interprétation de la probabilité postule que le résultat d’une expérimentation est produit par un certain ensemble de conditions génératrices. Lorsque l’on réalise à nouveau une expérimentation, on a à peu près les mêmes conditions génératrices. Dans ce cadre, on peut attribuer à cet ensemble de conditions génératrices une propension  de produire un résultat , cela veut dire que si on refait l’expérience infiniment sous les mêmes conditions on produira une séquence de résultats avec une fréquence relative limite . Dans le cas où l’expérience est déterministe, la propension serait égale à 0 ou à 1 pour chaque résultat.

Il existe un aspect central qui explique la propension à long terme, c’est la loi de grand nombre. Par exemple si une pièce est lancée plusieurs fois de manière répétée, de telle sorte que la probabilité d’avoir une pile est la même à chaque lancer, et les résultats sont probabilistes et indépendants, la fréquence relative des têtes sera (avec une probabilité élevée) proche de la probabilité des têtes à chaque lancer. On constate que les fréquences stables à long terme sont une manifestation de probabilités invariantes à cas unique.

La probabilité comme mesure de la croyance

Selon ce point de vue, les probabilités mesurent les degrés de croyance. Il s’agit de croyances sur l’occurrence d’un événement, la vérité d’une hypothèse ou la vérité d’un fait quelconque. Une probabilité de 1 représente notre certitude que quelque chose est vrai et une probabilité égale à 0 représente la croyance certaine que quelque chose est faux. Tout ce qui se trouve entre les deux implique une certaine incertitude quant à la vérité de l’événement ou de l’hypothèse.

Cette interprétation est subjective du fait qu’elle fait appel à notre croyance qu’une hypothèse ou un événement aura lieu. Suivant cette interprétation de la probabilité, on mesure la véracité ou la crédence des déclarations selon un agent approprié.

Agnès Buzyn, en tant que ministre de la santé, est-elle un agent approprié ? Oui, même si, pour évaluer le risque, elle s’est visiblement basée sur une étude l’ayant sous estimé.

Dans le cas où on dispose de plusieurs agents nous aurons autant d’interprétations de probabilité que d’agents appropriés. Ainsi, il en découle une question fondamentale : qu’est-ce qui rend un agent approprié ? Ce que nous pourrions appeler un subjectivisme sans contrainte n’impose aucune contrainte aux agents – tout le monde y va, et donc tout va.

Cependant, la pensée des agents appropriés doit au sens fort, être rationnelle. Par ailleurs, il existe une assimilation des subjectivistes de la probabilité à la logique en décrivant la probabilité comme « la logique de la croyance partielle ». Un agent rationnel doit être logiquement cohérent, maintenant pris au sens large, si l’agent obéit aux axiomes de probabilité.

Avec cette définition, on peut toujours évoquer la probabilité d’un événement unique, comme la définition de propension pas comme l’interprétation fréquentiste. En fait, l’avantage est de pouvoir considérer la probabilité comme un degré de croyance associé à n’importe quel énoncé. Contrairement aux deux définitions précédentes, on ne retrouve plus l’exigence de répétabilité des événements.

Il reste une question fondamentale au quelle il faudrait apporter une réponse, comment une telle théorie de probabilité subjective nous permet de distinguer un bon raisonnement d’un mauvais raisonnement d’agents appropriés. La seule logique consistante de raisonnement avec des dégrées de croyances subjectifs l’est, si est seulement si, ces dégrées de croyance satisfont les règles mathématiques de base de raisonnement probabiliste. La première étape qui apparaît évidente est l’assignation de degré de croyance à l’occurrence d’un événement ou à une hypothèse liée à une personne, comment on peut faire cela ? 

Pour répondre à cette question, deux pionniers de la probabilité subjective Frank Ramsey et Bruno de Finetti postulent qu’il y a une étroite relation entre le dégrée de croyance et l’action prise par un individu, la probabilité subjective a longtemps été analysée par le comportement au pari.

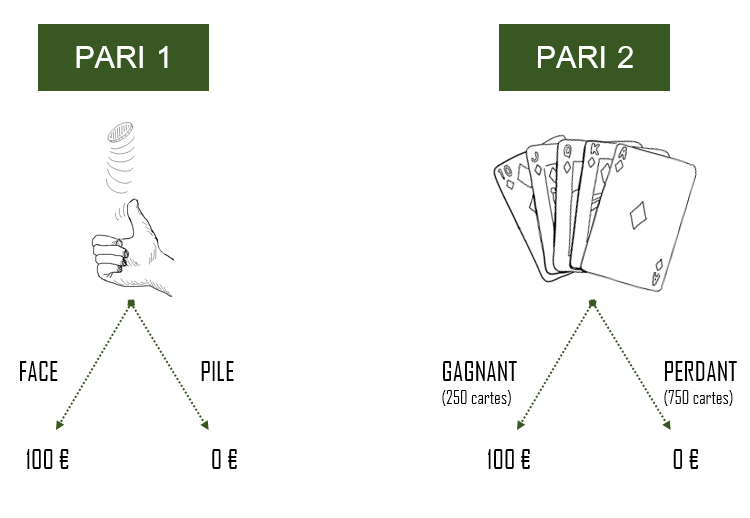
Supposons que nous sommes devant une situation où on est amené à choisir entre deux paris. Le premier pari consiste avec le choix entre pile ou face lors d’un lancement d’une pièce de monnaie, il y a un gain associé à chaque résultat obtenu de l’expérience de lancement de la pièce de monnaie si le résultat est pile on gagne 100€ si face, on ne gagne rien.

Frank Ramsey à gauche, Bruno de Finetti à droite

Le deuxième pari consiste en une expérience comme on peut la retrouver avec le principe de la loterie. On est amené à tirer une carte parmi 1000 cartes, il y a 750 cartes perdantes avec gain associé nul (0€) et 250 cartes gagnantes avec un gain de 100€.

La question à se poser est lequel des paris faut-il choisir ? Clairement il est plus judicieux de choisir le premier pari parce que la chance d’avoir un pile (1/2) est supérieur à la celle de tirer une carte gagnante (1/4). On croit qu’on a plus de chance à gagner en choisissant le premier pari que le deuxième. Maintenant, supposons qu’au lieu de 250 cartes gagnantes, on dispose de 750 gagnantes vs 250 cartes perdantes. Le choix du pari 2 est plus intéressant pour gagner les 100€. Dans un cas de figure avec 500 cartes gagnantes et 500 perdantes, on est indifférent sur le choix du pari parce que les chances de gagner les 100€ sont identiques dans les deux cas.

En deuxième lieu, tant que nous disposons d’une stratégie rationnelle d’assignation de probabilité à notre croyance, il faut que cette stratégie rationnelle soit consistante avec les règles de la théorie de probabilité. Pour répondre à cette question, Ramsey postule qu’aucune personne rationnelle n’acceptera volontairement un pari qui garantit de perdre de l’argent. C’est pour cela qu’il introduit la définition suivante :

La croyance cohérente

Un ensemble de croyance personnelles est dit cohérent s’il n’est pas ouvert à un contrat de perte sûr, on note que l’ensemble des croyances personnels n’a pas de contraintes en terme de respect de règles. C’est la raison pour laquelle il introduit une relation entre la théorie de la probabilité et la croyance personnelle. Un ensemble de croyance personnelles est dit cohérent, si est seulement, il satisfait les règles de la théorie de probabilité.

Un dernier point important de ce cadre de travail de l’interopération subjective de la probabilité décrit parfois comme probabilité bayésienne, est l’adoption du théorème de Bayes comme un principe général permettant l’apprentissage à partir de nouvelles expériences. La règle de Bayes est une formule mathématique de la théorie de probabilité permettant le calcul de probabilité conditionnelle.

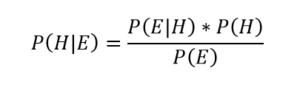
Règle de Bayes

P(H), la probabilité à priori d’une hypothèse H est le dégrée de croyance en H avant l’apprentissage de l’évidence E. P(H|E) est la probabilité à posteriori de l’hypothèse sachant que l’évidence E est vrai.  P(E|H) est la vraisemblance  de l’évidence E si l’hypothèse H est vrai.  P(E) est la probabilité totale de l’évidence E.

Le théorème de Bayes offre un modèle pour mettre à jour les probabilités où notre croyance initiale est la probabilité antérieure pour un événement, qui peut être mise à jour en une probabilité postérieure avec de nouvelles évidences. La règle de Bayes a une multitude d’application important dans l’inférence statistique, dans la théorie de décision et la théorie d’apprentissage. Elle joue un rôle central dans la pensée subjectiviste de la probabilité, c’est pour cela que les subjectivistes sont appelés parfois bayésiens.

Une dernière remarque portant sur la différence entre cette interprétation et la précédente est que les fréquentistes et préventionnistes ne mettent pas à jour les probabilités avec le théorème de Bayes, mais à partir de l’observation physique directe ou de l’analyse des propriétés physiques des objets impliqués dans le processus qui génère des résultats probabilistes.

La probabilité comme logique

Cette définition est en fait similaire à la précédente. La principale différence est qu’au lieu du degré de croyance, on parle du degré de soutien logique pour une hypothèse particulière. On considère cette interprétation selon laquelle les probabilités peuvent être déterminées à priori par un examen de l’espace des possibilités comme une généralisation de la logique classique.

Cependant, ils le généralisent de deux manières importantes : les possibilités peuvent se voir attribuer des poids inégaux (cela revient à E.T Jaynes qui a généralisé le principe d’indifférence en principe de maximum d’entropie) et les probabilités peuvent être calculées quelles que soient les preuves, symétriquement équilibrées ou non.

E.T Jaynes

En effet, l’interprétation logique, sous ses diverses formes, cherche à résumer en toute généralité le degré de soutien ou de confirmation qu’un élément de preuve  accorde à une hypothèse  donnée, que nous pouvons écrire comme C(H,E). Ce faisant, elle peut être considérée aussi comme une généralisation de la logique déductive et de sa notion d’implication, à une théorie complète de l’inférence dotée de la notion de « degré d’implication » qui relie E à H.

Ce que les probabilités logiques introduisent, c’est un moyen de gérer l’incertitude. Si une probabilité est un nombre différent de 0 ou 1, il y a un certain niveau d’incertitude quant à la crédence de l’énoncé. L’incertitude augmente à mesure que la probabilité s’éloigne de 0 et de 1 en se rapprochant de 0,5. Elle est d’autant plus grande que la probabilité est exactement de 0,5, car les preuves sont également indécises quant à la véracité de la déclaration.

Le théorème de Bayes joue encore une fois un rôle important dans la mise à jour des probabilités sauf qu’on est plus contraint à notre priori initial, on ne peut pas faire appel à des choses vagues comme notre intuition. Cette interprétation des probabilités peut être qualifiée comme Bayésienne objective, alors que la précédente comme Bayésienne subjective

Conclusion

Chacune des interprétations présentées précédemment essaye de saisir une idée cruciale de son concept, sans parvenir à lui rendre pleinement justice.. En ce sens, les interprétations ci-dessus peuvent être considérées comme complémentaires, néanmoins les probabilités bayésiennes et fréquentistes sont les plus connues de nos jours. De même qu’il existe une sorte de rivalité entre ces deux conceptualisations des probabilités dans plusieurs domaines et disciplines surtout dans l’inférence statistique et à la théorie de décision. Nous essayerons dans le futur d’aborder les points de différence entre la pensée bayésienne et la pensée fréquentiste d’un point de vue pratique et non épistémologique.