Le théorème de Bayes appliqué à l’archéologie [1/2]

Aujourd’hui je voudrais vous parler de la théorie des probabilités. Pour cela, prenons l’exemple de certains artéfacts archéologiques dont l’origine semble inexplicable en suivant l’histoire « classique ».

À partir des années 1880, Flinders Pétrie, archéologue, égyptologue et scientifique reconnu participe aux fouilles autour de la pyramide de Gizeh. Lors de ces fouilles, il trouve un objet étrange qui s’apparente à une carotte issue d’un ancien forage.

Il se demande quel processus a bien pu produire un tel objet ? Quand les habitants de l’Egypte antique avaient besoin de percer la pierre, ils utilisaient des cylindres métalliques (fraises) et de l’abrasif. Une fois le trou réalisé, le cylindre métallique est enlevé et, avec lui, une carotte de pierre :

Monsieur Pétrie étant un archéologue expérimenté, il demanda l’avis d’un ingénieur sur la nature de cet artéfact. Les difficultés pour comprendre comment un tel objet avait pu être fait ne faisaient que commencer, voici pourquoi :

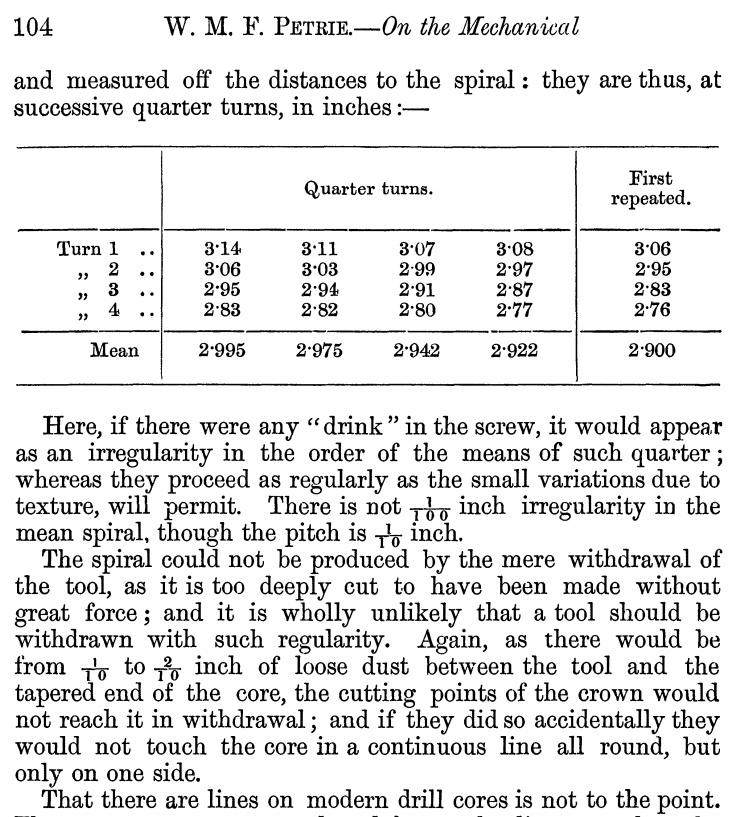
• le canal présent sur l’artéfact (aussi connu en tant que Cylindre Numéro 7 de Pétrie, soit UC-16036) semble avoir une forme géométrique très précise – une spirale, en l’occurrence, avec un pas presque constant (suivant la description de Pétrie),
• si nous supposons que c’est le résultat d’un fraisage (et c’est le cas), les lignes ont été laissées par un outil extrêmement puissant qui n’a malheureusement pas été retrouvé,
• personne ne savait (et on ne sait toujours pas) construire des outils aussi puissants.

Cette suite logique a été complétée par des nombreux chercheurs d’histoires alternatives…

Voici la photo de cet objet mystérieux (au moment de la publication de notre article, la photo est disponible ici : https://discovery.ucl.ac.uk/id/eprint/1468795/4/The_Petrie_Museum_of_Egyptian_Archaeology.pdf) :

En quoi tout cela peut nous intéresser ? Posons nous la question suivante : devons-nous changer notre avis sur l’histoire de l’Egypte antique et sur les technologies disponibles il y a des milliers d’années ou non ?

Je vous propose un moyen pour calculer la réponse… puis de voir la réponse d’archéologues contemporains dans un second article.

Comme vous le savez (si non je vous invite à lire notre article https://ithealth.io/les-probabilites-a-la-lumiere-de-lactualite/), la théorie de probabilité peut être appliquée aux jugements logiques. Dès lors, je vous propose un « cours » intensif de 10 minutes appliqué à la découverte de Pétrie. Cette approche vous sera utile pour d’autres jugements.

Probabilités en 10 minutes

Comme vous le savez, la probabilité permet de décrire notre niveau de certitude ou d’ignorance d’un événement donné (probabilité Bayesienne).

Laplace a donné la définition suivante à la probabilité : « une fraction, dont le numérateur est le nombre des cas favorables et dont le dénominateur est le nombre de tous les cas possibles ».

Nous pouvons la visualiser avec le graphique suivant:

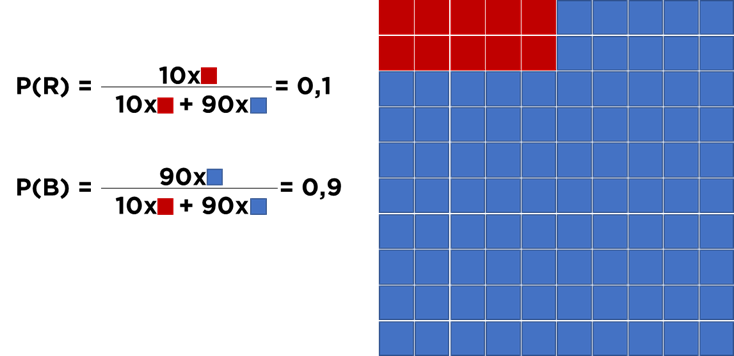
Dans notre exemple, je peux dire que j’ai 0,1 de chances que l’événement marqué en « rouge » va se produire et 0,9 de chance que l’évènement « bleu » va se produire.

Attention : la somme de la probabilité des événements qui « couvrent » l’ensemble des possibilités est égale à 1 (P(R)+P(B)=1).

Maintenant, ajoutons une nouvelle définition : la probabilité conditionnelle. Pour comprendre de quoi il s’agit, supposons qu’il existe deux types d’événements supplémentaires : « foncés » et « clairs ». Supposons que vous observez un événement « foncé », quelle est la chance qu’il soit également « rouge » ? Notre condition sera : on ne garde que les « foncés ». Alors, on jette les « clairs ». Dans ce cas, la probabilité de retrouver le rouge à la condition qu’il soit « foncé » est un ratio de « rouges foncés » à tous les « foncés » et égale à 0,25. Cf l’image dessous :

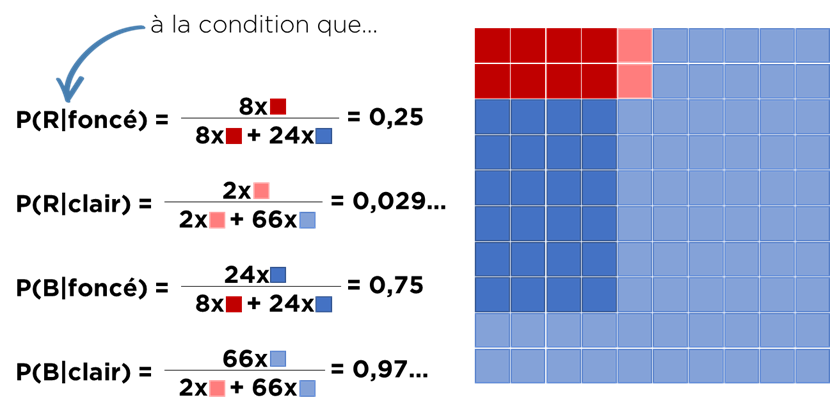
Maintenant je vous propose le fameux théorème de Bayes qui énonce la possibilité de convertir une probabilité conditionnelle à une autre en utilisant cette formule générale :

P(X|Y) x P(Y) = P(Y|X) x P(X)

Nous pouvons maintenant prouver le théorème de Bayes en utilisant notre exemple :

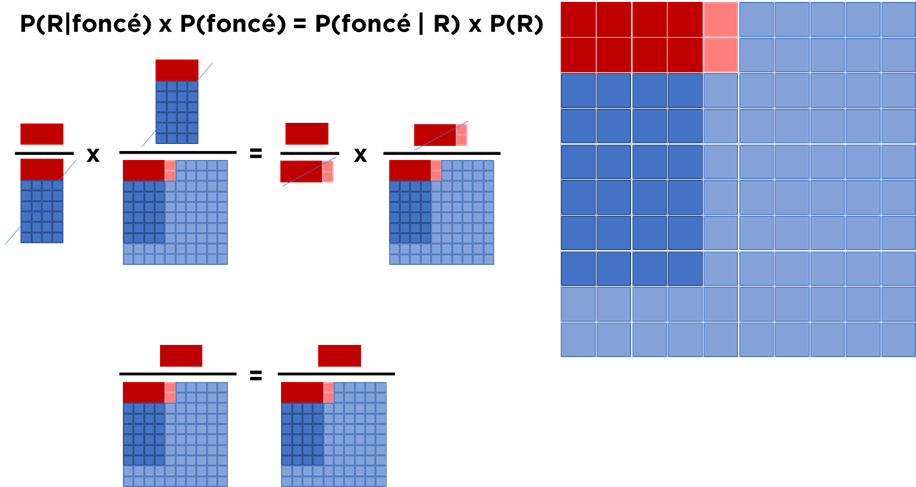
Exemple. Supposons que chaque matin je sors de chez moi en même temps que mon voisin qui semble presque toujours savoir si il y aura une pluie aujourd’hui. En observant assez longtemps, je peux conclure que :
(1) il pleut approximativement 1 jour sur 5, donc P(pluie) = 0,2
(2) le voisin sort avec le parapluie 3 jours sur 10, donc P(parapluie) = 0,3
(3) quand il pleut, le voisin prend son parapluie 7 fois sur 10, donc P(parapluie|pluie) = 0,7
Donc… si ce matin vous voyez mon voisin avec son parapluie, les chances qu’il pleuve aujourd’hui sont les suivantes :
P(pluie|parapluie) = P(parapluie|pluie) * P(pluie) / P(parapluie) = 0,7 * 0,2 / 0,3 = 0,466… ~ 46%…

Exemple plus complexe. Parlons de maladies. Supposons qu’une personne vienne de faire un test de la maladie X, test finalement positif. Quelle est la chance que la personne soit vraiment malade ?
(1) Prenons l’incidence de la maladie à 1% : P(maladie X) = 0,01
(2) Pour les tests supposons que nous connaissons le ratio de tests positifs sur le nombre total de tests effectués, P(test +) = 0,05
(3) Nous avons besoin d’un paramètre supplémentaire – taux de tests positifs à la condition de maladie (i.e. nombre de tests correctement positifs pour les malades) : P(test +|maladie X)=0,9 (ce chiffre dépend de la fiabilité de notre système de tests)
Maintenant aux chances de la personne en question :
P(maladie X|test +) = P(test +|maladie X)*P(maladie X)/P(test +) = 0,9 * 0,01/0,05 = 0,18 = 18%… seulement 18% !
C’est pour cela que les médecins en général font un second test si le premier est positif !

Acquis ? Avançons…

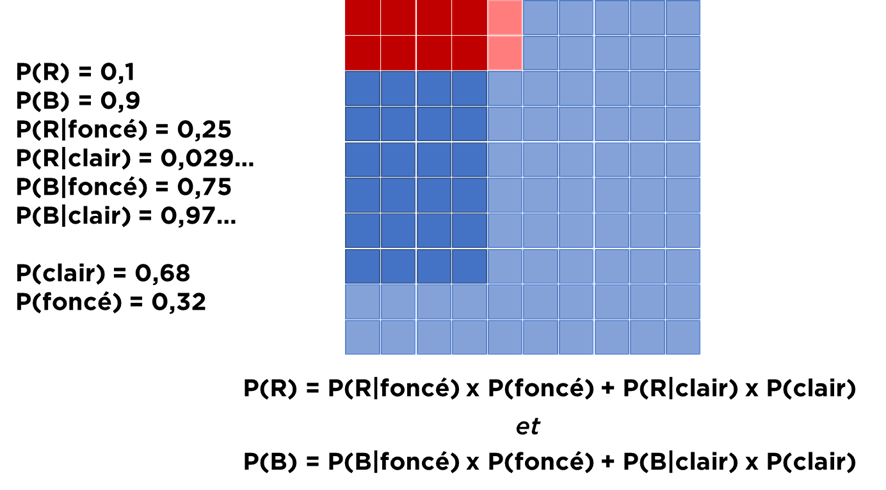
Voici un nouveau cas : supposons qu’il nous faut estimer P(R) (comme si on ne le connaissait pas) mais nous connaissons P(R|foncé), P(R|clair), P(foncé) et P(clair).

La probabilité d’évènement P(R) est une somme pondérée de probabilités conditionnelles : P(R) = P(R|foncé) x P(foncé) + P(R|clair) x P(clair).

Vous pouvez le vérifier vous-même, cf. l’image ci-dessous :

Exemple. Supposons que devant vous il y a deux vases identiques avec des bonbons et vous savez que dans un vase il y a 60% de vos bonbons préférés et dans l’autre – que 10%, sans pour autant connaître la répartition dans les deux vases.
Vous avez donc le droit de piocher qu’une seule fois. Quelle est la chance que vous allez sortir votre bonbon préféré ?
P(préféré) = P(préféré|vase 1) *P(vase 1)+ P(préféré|vase 2) *P(vase 2)=0,6*0,5+0,1*0,5=0,3+0,05=0,35, soit 35%.

Nous allons appliquer notre connaissance des probabilités afin de découvrir la réponse : si oui ou non il existait des technologies incroyables dans l’Egypte antique…

To be continued…

La suite : https://ithealth.io/le-theoreme-de-bayes-applique-a-larcheologie-2-2/