Hacking et magie : la programmation statistique c’est cool

Un jour, j’ai du travailler sur un algorithme assez pointu pour la prédiction des courbes de demande (price management). J’ai rapidement compris que les algorithmes de Machine Learning ne pourraient pas le résoudre. Dans ma tête tournait une pensée « tu dois faire de la statistique », mais pour être franc, « je n’ai jamais su faire et puis, j’ai tout oublié ».

Pourquoi statistique : peu de données + beaucoup d’erreurs + besoin de pouvoir estimer l’erreur de la prédiction. Il faut, donc, un modèle compréhensible qui ne permet pas seulement donner une prédiction, mais surtout une distribution des solutions potentielles. Dans mon cas, il fallait dire « je suis 90% sûr que votre prix est trop élevé », par exemple.

Comme par hasard, chaque jour je tombais sur les articles de modèles statistiques, modèles hiérarchiques, etc – et un soir en regardant une présentation j’ai remarqué un quadrigram MCMC (Markov Chain Monté Carlo). Une heure plus tard j’installais la bibliothèque PyMC (pour Python) pour tester cette approche sur mon PC.

Une remarque : il y a plein d’autres bibliothèques pour tous les langages et il y a même des langages spécialisés. Par la suite, j’ai implémente MCMC basique en Java en une nuit… Je ne conseille pas une bibliothèque précise dans cet article.

Vous pouvez imaginer – je suis tombé amoureux. Je ne peux pas dire que tout était facile, mais le début du cours de base de la théorie de probabilité est suffisant pour créer des modèles qui fonctionnent. Au pire – quelques heures de révision – et vous êtes prêt pour commencer.

Tour roule, donc. Mais les points négatifs dans tout ça ? Bien, il y en a au moins un : la lenteur. Rien ne peut remplacer un bon mathématicien qui prendra toutes les intégrales analytiquement et en fera un algorithme qui calcule le résultat en une milliseconde. MCMC réalise le calcul par la « bruteforce ».

Théorie

Pour créer votre algorithme avec MCMC vous devez définir 3 choses :

• Les paramètres inconnus de votre modèle et ce que vous connaissez concernant ces paramètres (valeur minimal/maximal ou distribution de probabilité que vous connaissez « à priori »).
• Le modèle : les interactions de ces paramètres avec les données que vous avez. I.e. comment, à votre avis, vous pouvez obtenir la prédiction.
• L’erreur applicable à votre modèle (i.e. pour quelle cause vos observations ne correspondent pas à vos prédictions).

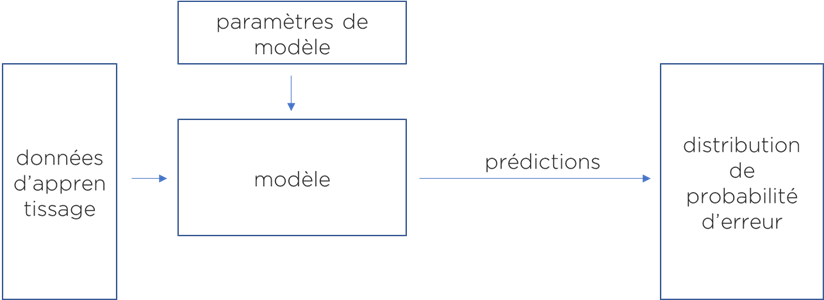
Cela ressemble à un algorithme classique de machine learning (https://ithealth.io/machine-learning-une-explication-facile/), sauf que vous allez pouvoir définir les interactions entre les paramètres vous-mêmes et obtenir un modèle qui a du sens du point de vue métier.

Je vais prendre l’exemple d’un livre génial disponible en ligne et sur Amazon : « Bayesian Methods for Hackers » (https://github.com/CamDavidsonPilon/Probabilistic-Programming-and-Bayesian-Methods-for-Hackers) : supposons que vous voulez comprendre, quand (et si) vous avez commencé à recevoir plus ou moins de messages de la part d’une personne. Pour ce modèle vous avez besoin de 3 paramètres : le jour du changement d’attitude (inconnu, mais entre les début et fin de données), quantité moyenne de messages par jour avant cette date et quantité moyenne de messages par jour après cette date. La distribution d’erreur suit la loi de Poisson.

Le résultat de ce modèle, contrairement à d’autres méthodes de Machine Learning sera une distribution de probabilité de chaque paramètre, i.e. vous pouvez donc obtenir le modèle, mais aussi, voir à quel niveau ce modèle est « certain » du résultat :

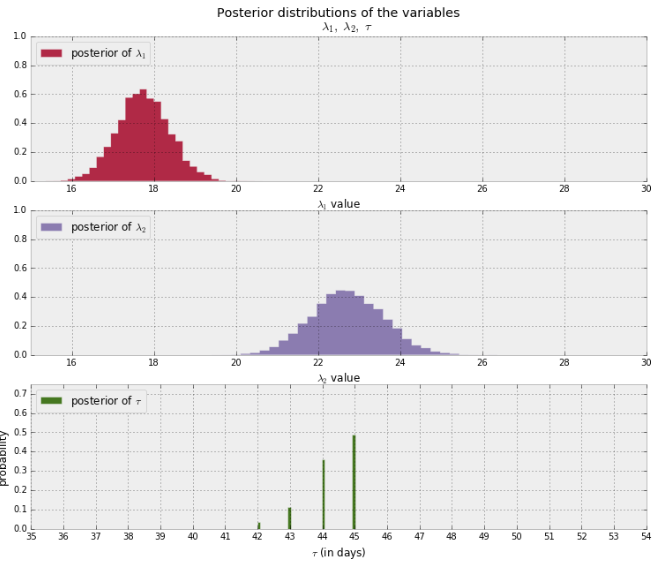
Le résultat de cet algorithme : il y a un changement évident (augmentation de nombre de messages par jour) autour du jour 45.

Certes, l’approche est relativement facile à comprendre, c’est de la probabilité (https://ithealth.io/un-algorithme-parfait/), c’est explicable, ça donne plus d’information, mais comment ça fonctionne ?

En fait, les algorithmes actuellement utilisés sont assez complexes, mais l’idée qui a rendu tout cela possible est relativement simple. Tout a commencé avec l’algorithme suivant de Nicholas C. Metropolis (1953) et Wilfred K. Hastings (1970) :

• choisir les paramètres de modèle,
• faire un « petit pas » dans une direction choisie au hasard,
• si le modèle avec les nouveaux jeux de paramètres explique mieux les données, accepter ce pas, sinon – si le nouveau modèle est pire que précédent – la décision d’accepter ce nouveau pas ou bien de revenir vers les paramètres précédents est stochastique et dépend du ratio d’erreurs de ces modèles,
• repéter (à partir de choix de pas).

Il a été prouvé que ce processus permet d’estimer la vraie distribution « à posteriori » des paramètres du modèle.

Ce processus simple permet aux humbles développeurs de toucher le monde de calcul statistique sans se prendre trop la tête.

« Show me your code » ou pratique pour les courageux

Pour vous prouver que la statistique est accessible, nous allons utiliser un exemple de prédiction du niveau CO2 des voitures (au moment de publication, le fichier de données utilisé est disponible « ici »).

Notre modèle sera linéaire et nous allons essayer de prédire le champ CO2EMISSIONS via ENGINESIZE, CYLINDERS et FUELCONSUMPTION_COMB. Pour faire ce modèle, il nous faut 5 paramètres (inconnus) qu’on va combiner par la suite. Les paramètres de régression linéaire : c0..c3 sont quelconques (nous n’avons pas de « prior »). Par contre, pour prendre en compte les erreurs de notre modèle, on utilisera la loi Normale qui nécessite encore un paramètre – sigma qui doit être positif :

with Model() as model:
    c0 = Flat('c0')
    c1 = Flat('c1')
    c2 = Flat('c2')
    c3 = Flat('c3')
    sigma = HalfFlat('sigma')

Flat – paramètre quelconque, HalfFlat – paramètre positif.

Une fois que nous avons défini nos paramètres, nous pouvons faire une prédiction (ici j’ai enlevé les subtilités techniques liés à l’extraction de données – on les verra dans le listing complet) :

    predict = c0 + <axe 1> * c1 + <axe 2> * c2 + <axe 3> * c3

Maintenant, nous avons notre prédiction (pour chaque ligne de données), mais nos « observations » proviennent du monde réel et il sera difficile de les prédire exactement, donc nous allons permettre une erreur qui suit la loi Normale (c’est classique) :

    err = Normal('err', mu=predict, sigma=sigma, observed=<axe à prédire>))

Ce que nous disons ici : nous avons prédit l’axe « à prédire » (CO2EMISSIONS) par une distribution Normale (Gaussienne) avec une moyenne égale au résultat de notre modèle et sigma égal à un paramètre inconnu.

Voici le code complet avec toutes subtilités de conversion de types, imports, etc (j’ai pris 5000 points pour modéliser nos distributions + 1000 supplémentaires pour qu’algorithme s’autoconfigure, magie !) :

import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
from pymc3 import *

df = pd.read_csv("FuelConsumptionCo2.csv")

with Model() as model:
    c0 = Flat('c0')
    c1 = Flat('c1')
    c2 = Flat('c2')
    c3 = Flat('c3')
    sigma = HalfFlat('sigma')
    predict = c0 + np.asarray(df['ENGINESIZE']) * c1 + \
                   np.asarray(df['CYLINDERS']) * c2 + \
                   np.asarray(df['FUELCONSUMPTION_COMB']) * c3
    err = Normal('err', mu=predict, sigma=sigma, \
                        observed=np.asarray(df['CO2EMISSIONS']))
    step = NUTS()
    trace = sample(5000, tune=1000, cores=1, step=step)

Une fois la simulation terminée, nous pouvons regarder les résultats. On verra la certitude de notre modèle par rapport aux différents coefficients :

plots.traceplot(trace)
fig = plt.gcf()
fig.savefig("trace-cars.png")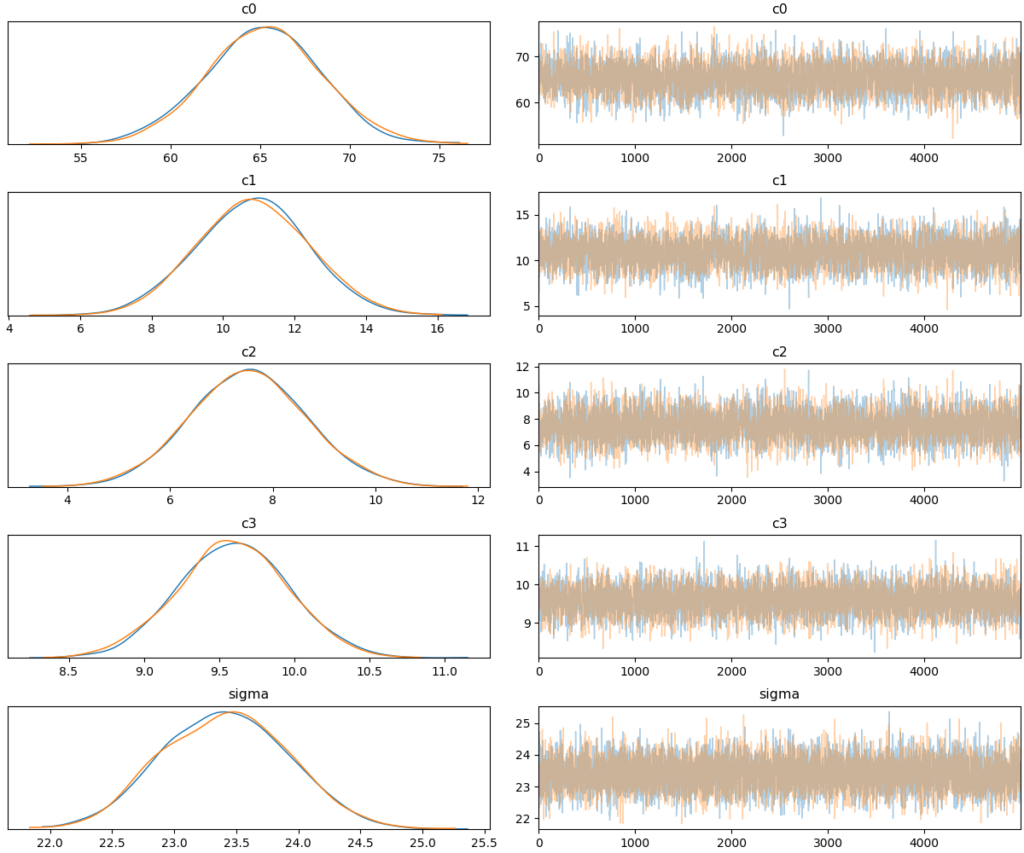

Conclusion : pour notre modèle, nous n’avons pas seulement obtenu les paramètres qui prédisent le mieux les résultats, mais surtout l’information concernant l’incertitude de notre modèle à propos des paramètres. On pourra utiliser cette information pour analyser la qualité de prédiction !

Nous pouvons voir que les distributions pour nos coefficients sont assez larges. Il ne faut pas attendre à une haute qualité de résultat avec ce modèle, surtout pour les valeurs importantes des paramètres, mais essayons-le !

J’ai choisi les paramètres pour ce test (pour faire une prédiction pour une nouvelle voiture) :

ENGINESIZE = 3.5
CYLINDERS = 6
FUELCONSUMPTION_COMB = 12

Maintenant nous pouvons « extraire » les distributions et faire le calcul pour obtenir la distribution des prédictions moyennes :

c0 = trace['c0']
c1 = trace['c1']
c2 = trace['c2']
c3 = trace['c3']

predict = c0 + c1*ENGINESIZE+c2*CYLINDERS+c3*FUELCONSUMPTION_COMB
plt.hist(predict, bins=60)

Le résultat de calcul n’est pas mauvais – la distribution est située entre 261 et 266, l’incertitude est minime. Cela veut dire que notre modèle a eu suffisamment d’information pour trouver les paramètres qu’il faut (pour ce cas précis) :

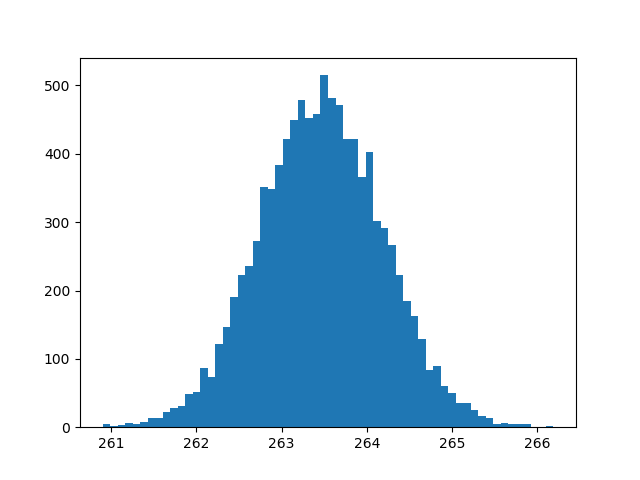
Par contre, nous avons vu l’histogramme des prédictions moyennes, sans prendre en compte les erreurs liées aux cas que notre modèle ne peut pas prédire. Prenons en compte les erreurs (loi Normale, vous vous rappelez ?). Ici, je génère pour chaque point de distribution de paramètres 50 valeurs possibles :

sigma = trace['sigma']
predictErr = [value \
              for i in range(predict.size) \
              for value in np.random.normal(predict[i], sigma[i], 50)]
plt.hist(predictErr, bins=300)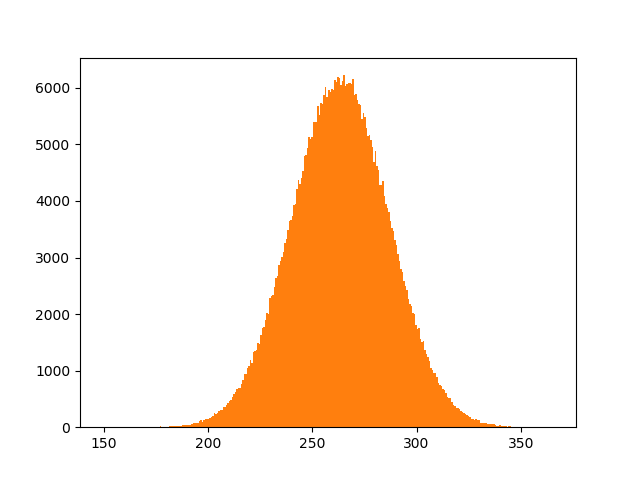

Aïe ! La prédiction n’est pas si précise … Vu que notre modèle est très simple et n’utilise que 3 paramètres, la distribution du résultat est assez mauvaise. Par contre, c’est bien, au moins nous savons que pour ce point, notre modèle n’est pas en capacité de donner la précision désirée.

Nous pouvons maintenant essayer un modèle plus-plus : modèle hiérarchique. Cette fois je vais dire que chaque voiture a une marque et chaque marque a ses propres paramètres d’émission de CO2, mais tous ces paramètres proviennent de même distribution globale, i.e. toutes marques sont proches en quelque sorte, sauf si on arrive à prouver le contraire par les données.

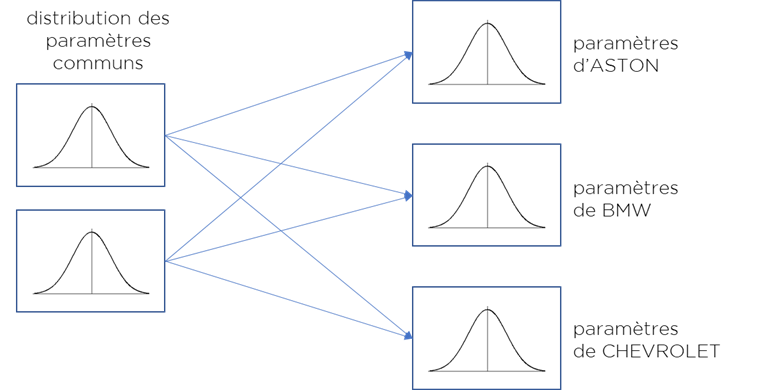
Nous allons prendre la liste unique des marques :

brands = df['MAKE'].unique()

Puis, dans notre modèle nous allons définir la distribution commune à toutes nos marques :

with Model() as model:
    c0mu = HalfFlat('c0mu')
    c0sigma = HalfFlat('c0sigma')
    c1mu = HalfFlat('c1mu')
    c1sigma = HalfFlat('c1sigma')
    c2mu = HalfFlat('c2mu')
    c2sigma = HalfFlat('c2sigma')
    c3mu = HalfFlat('c3mu')
    c3sigma = HalfFlat('c3sigma')
    sigma = HalfFlat(brand + 'sigma')

Mais chaque marque aura ses propres paramètres liés à cette distribution commune :

    for brand in brands:
        c0 = Normal(brand + 'c0', mu=c0mu, sigma=c0sigma)
        c1 = Normal(brand + 'c1', mu=c1mu, sigma=c1sigma)
        c2 = Normal(brand + 'c2', mu=c2mu, sigma=c2sigma)
        c3 = Normal(brand + 'c3', mu=c3mu, sigma=c3sigma)
        brandData = df[df['MAKE'] == brand]
        predict = c0 + np.asarray(brandData['ENGINESIZE']) * c1 + \
                  np.asarray(brandData['CYLINDERS']) * c2 + \
                  np.asarray(brandData['FUELCONSUMPTION_COMB']) * c3
        err = Normal(brand + 'err', mu=predict, sigma=sigma, \
                     observed=np.asarray(brandData['CO2EMISSIONS']))

C’est tout ! Après le calcul, nous allons obtenir les paramètres pour chaque marque et on pourra les comparer :

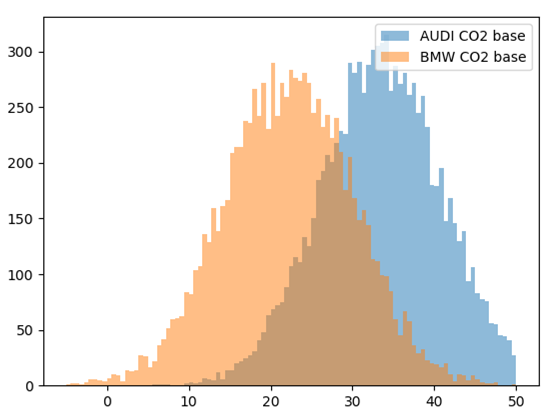
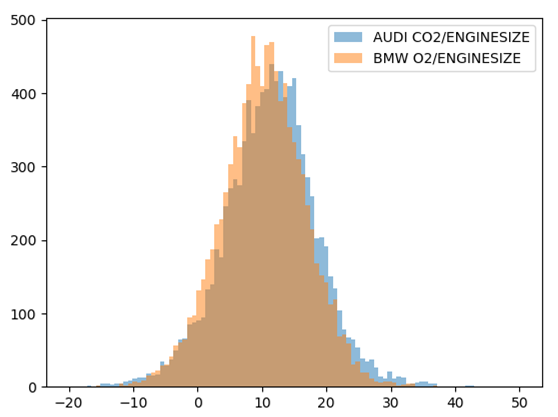
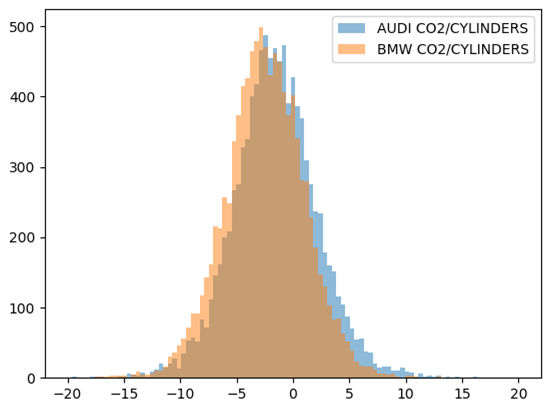
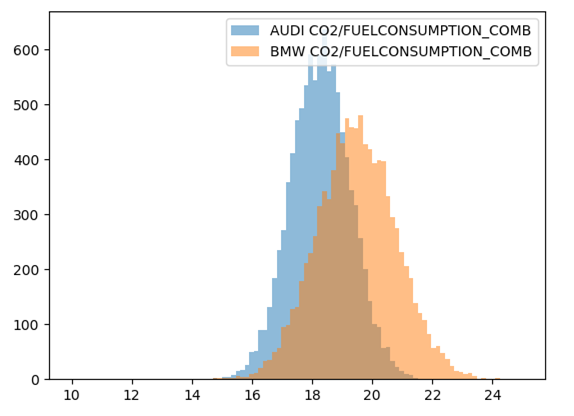
De plus, nous pouvons observer que l’erreur (paramètre sigma) dans notre modèle hiérarchique s’est diminué par le facteur de 2x :

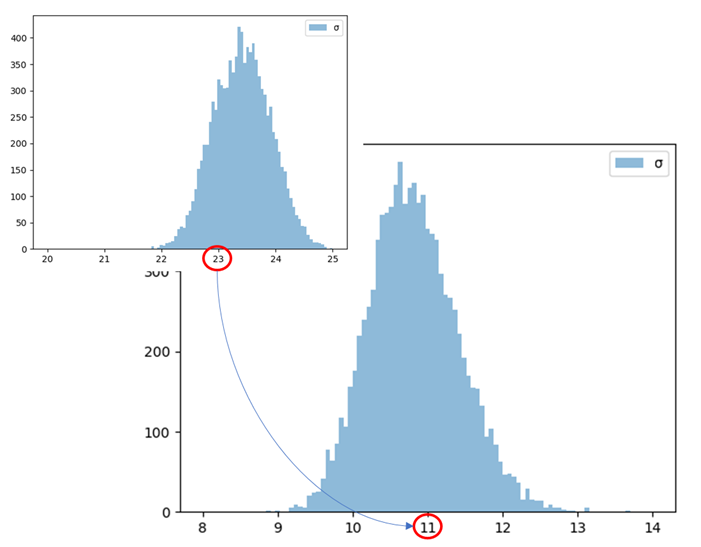
Conclusions

• Nous avons appris une approche pour composer les modèles statistiques et les configurer en utilisant un minimum d’énergie cérébrale.
• Cette approche ne permet pas seulement de trouver une solution qui explique le mieux nos données comme dans la plupart des méthodes de machine learning, mais surtout d’estimer la qualité de nos prédictions. Très utile.

Bonne santé à vous et à vos systèmes !