If Einstein had enough observational evidence to single out the correct equations of General Relativity in the first place, then he probably had enough evidence to be damn sure that General Relativity was true.
Eliezer Yudkowsky,
https://www.lesswrong.com/posts/MwQRucYo6BZZwjKE7/einstein-s-arrogance

Le problème de Behrens-Fisher (ou problème d’égalité) est bien connu. Assez certainement, vous avez appris à l’école au moins l’une des méthodes pour résoudre ce problème (un ami à moi collectionne des solutions incorrectes à ce problème – il a une sacrée liste).

Disclaimer : vu que c’est un blog et pas du tout une publication scientifique, je me permets de prendre les définitions « au léger ». Ce post est juste un braindump.

En quoi consiste le problème ?

Supposons que vous avez mesuré quelque chose deux fois et maintenant vous voulez savoir si les deux mesures sont les mêmes :

vous avez changé la couleur de bouton sur le site web et vous voulez savoir si cela augmente la conversion de clients ou pas ;
vous avez inventé un nouveau produit contre COVID (c’est toujours à la mode, le sujet ?) et vous voulez savoir si votre produit est meilleur que placebo ou autres produits sur le marché ;
vous êtes un fan de la physique et vous vous posez la question si les ondes gravitationnelles se propagent avec la vitesse de lumière (ce que les scientifiques pensent, mais dans les fameux tests de LIGO les deux sont arrivés au différents moments, donnant la différence minuscule) ;
etc

En gros, nous avons fait deux tests A et B qui mesurent une certaine propriété de deux objets différents et nous voulons savoir si les deux valeurs sont les mêmes.

Cela n’a pas de sens

Pour expliquer, à quel point cela n’a pas de sens, je vous propose un exercice mental.

Sur la planète Bidon les scientifiques essayent de mettre une sphère parfaite sur un plateau idéalement horizontal et qui n’exerce aucune force de friction, de telle manière que la sphère reste immobile.

Un inventeur, Elon Task affirme qu’il a bien réussi de créer un appareil qui pouvait installer une telle sphère. Elon propose aux scientifiques de conduire le test ultime de vitesse zéro.

Afin d’éliminer toutes les mesures (et donc forces externes), les scientifiques ont mis en place le test suivant :

la sphère sera installée sur la surface parfaite, mais à gauche et à droite de la surface il y aura deux trous ;
si Elon Task n’arrive pas à installer la sphère come prévu, un jour ou l’autre elle tombera dans l’un des trous ; ainsi les scientifiques auront encore quelques milliards de bidon-dollars pour continuer sa recherche.

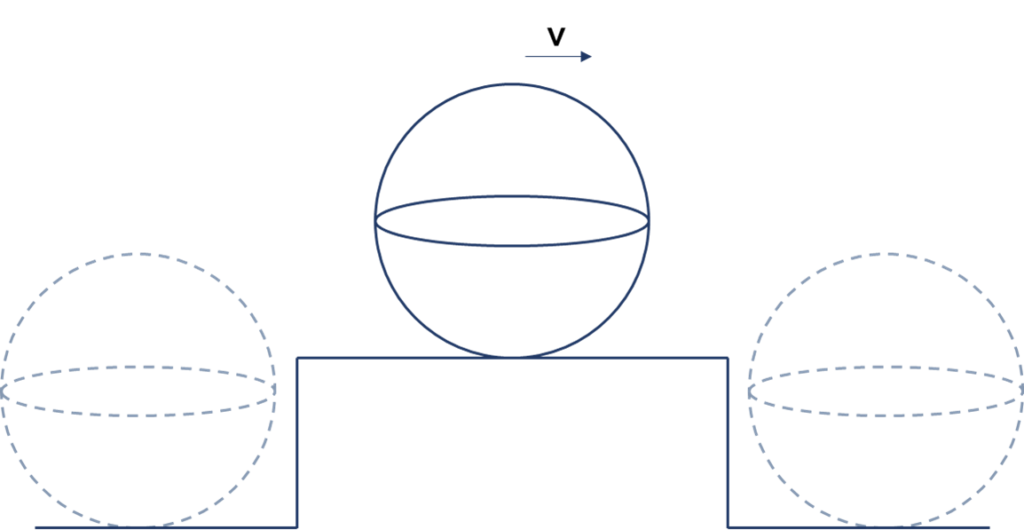
Le temps passe et la sphère reste toujours sur le podium, mais les scientifiques ne se précipitent pas pour annoncer Elon Task gagnant. Ils disent : « cela juste prouve que la vitesse est effectivement minuscule, mais la probabilité que M. Task a réussi d’installer la sphère immobile est strictement zéro, donc impossible ».

Même si ce n’est pas très juste vis-à-vis de M. Task, c’est bien correct. Chaque heure que la sphère passe sur le podium limite sa vitesse (v<taille podium/temps), mais il ne sera jamais possible de prouver que la vitesse est précisément zéro.

Cet exemple montre que même dans le monde parfait, même si on compare un paramètre à zéro, il sera compliqué de prouver que le résultat EST ZERO. Il est toujours infiniment plus probable que les deux choses soient différentes.

Du coup, ça n’a pas de sens de dire que la vitesse d’onde gravitationnelle est la même que la vitesse de lumière. Même si les deux sont différentes de moins de 0,0000000000001% (https://www.forbes.com/sites/startswithabang/2019/07/06/ask-ethan-why-do-gravitational-waves-travel-exactly-at-the-speed-of-light/) :

C’est comme si vous jouez en fléchettes infiniment minuscules et vous essayez de viser la fléchette précédente. Essayez vous-mêmes.

Pourtant, je n’ai rien dit de nouveau ici…

On ne se baigne jamais deux fois dans le même fleuve. …
Héraclite

Le fait que ça n’a pas de sens n’a pas de sens

Mais en fait… si on continue de la même manière, nous pouvons aussi dire que la vitesse de lumière n’est pas égale à elle-même. Cela doit être évident car nous vivons dans le monde ou rien n’est égal à rien. Pourquoi la vitesse de lumière doit-elle être constante ? Ce n’est pas possible à prouver non plus.

Il serait également impossible de se baigner une fois dans le même fleuve, car le fleuve lui-même et l’eau qu’il contient se modifient constamment
Cratyle

Le problème est mal posé, donc, il manque de la régularisation

Je commence par quelques faits qui n’ont rien de commun :

Il existe une encyclopédie des suites de nombres de Sloan (c’est plus amusant que vous pouvez penser) et si on analyse les séquences dans cette encyclopédie, on trouve que certains nombres sont beaucoup plus « populaires » que les autres. C’est connu en tant que « Sloan’s gap ». Pourquoi existe-t-il ce gap?

Les physiciens n’aiment pas les « petites différences » entre les constantes. Pourquoi ?

Les physiciens des particules pensent également qu’une théorie est belle si elle ne contient que des nombres « naturels » – des nombres proches à 1. On dit d’un nombre non naturel qu’il est « ajusté ».
Lost in Maths, Sabien Hossenfelder

Un certain Solomonoff a inventé une machine qui en absolue peut apprendre tous sur le monde qui nous entour. Solomonoff a (apparemment) fait quelques petites fautes, mais malgré tout cette machine est plus puissante que tous les algos ML que nous avons aujourd’hui.

Mon hypothèse est que dans le problème de Behrens-Fisher il manque une probabilité conditionnelle (prior, si vous voulez). Ce n’est pas par hasard que nous comparons deux paramètres – c’est parce que nous construisons une certaine « théorie » (dans le sens de Solomonoff).

Pour toutes les théories Solomonoff a inventé un prior (pour rappel – longueur de programme la plus courte pour la machine de Turing pour produire les prédictions de la théorie). Le problème est que Solomonoff a absolutisé cette notion et en absolue ce problème ne peut pas être résolu.

Et si nous jouons en Bayésianisme ? On ne va pas prendre n’importe quelle machine de Turing, mais un encodage qui se prouve utile sur une multitude de problèmes que nous avons résolu ?

J’imagine que :

la liste de valeurs que nous pouvons utiliser dans la théorie sera discretisée ;
les valeurs « ajustées » (comme 0.999998) seront pénalisées ;
les autres valeurs, « utiles » seront plus probables ;
la théorie qui utilise qu’un seul paramétre sera au moins un bit plus courte que la théorie avec deux paramétres.

J’ai décidé de choisir un encodage binaire (un peu surréel) – pour chaque valeur il y a un prior qui se diminue exponentiellement avec le nombre de chiffres binaires (sur graphique : probabilité vs valeur) :

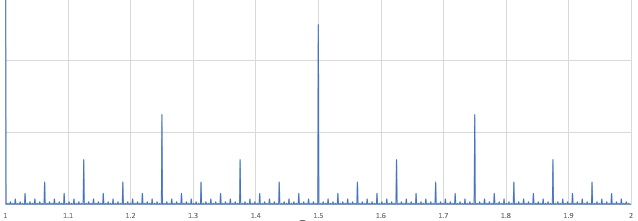
Note : oui, je peux expliquer, pourquoi binaire et pas décimal – il semble capter les nouveau chiffres significatifs plus vite que n’importe quel autre encodage.

Le prior en 2D : même si les deux tests A et B sont indépendants, le fait que les deux appartiennent au même modèle les rendra dépendants via prior sur le modèle (modèle doit « stocker » moins de bits) :

Si notre postériori dans le cas de valeurs continues ressemblait à cela :

…il se changera à cela une fois nous prenons en compte le prior sur la simplicité de modèle (chaque « pique » est une « delta ») :

Maintenant la probabilité que le paramètre A est égal au paramètre B n’est plus jamais zéro. La probabilité est égale à la somme des valeurs sur la diagonale et divisée par la somme sur l’ensemble de surface. Et oui, diagonale est toujours « favorable » car donne la « théorie la plus simple ».

Je vais ignorer les détails car nous avons ignoré tant de choses, que les questions de calcul de prior depuis le nombre de bits me semble superficiel dans ce contexte (mais pas simple en absolue).

N’hésitez pas à commenter.

Bonne santé à vous et à vos modèles.