Machine Learning : une explication facile

As far as the laws of mathematics refer to reality, they are not certain, and as far as they are certain, they do not refer to reality.

A. Einstein

Si vous suivez l’actualité des entreprises, vous entendez régulièrement parler d’IA, de réseaux de neurones (neural networks), de SVM, d’arbres de décision, de boosting, de bagging, de XGBoost, de biais, de surapprentissage ou encore de régression. Le sens vous échappe ? Vous vous perdez entre la classification et la clusterisation ? En 15-20 minutes, nous allons vous aider, du moins, essayons !

Commençons par les problèmes que vous pourriez avoir envie de résoudre :

• Vous cherchez à prédire le nombre de visiteurs de votre magasin ?
  Vous voulez savoir combien du temps prendra une opération ?
  C’est une régression. Le nom est donné pour des raisons historiques. En effet, Francis Galton en utilisant la méthode de prédiction de la taille d’un humain a trouvé une « régression » vers la moyenne.
• Vous cherchez à comprendre, quel type de client est devant vous ?
  Vous classifiez des images ou du texte ?
  C’est une classification. Contrairement à la régression, vous n’obtiendrez pas un chiffre, mais une groupe/class (avec une probabilité associée).
• Vous voulez comprendre, combien de types de clients vous avez ou comment codifier les tailles des tee shirts ?
  C’est une segmentation (clustering). Contrairement à la classification, nous cherchons pas à assigner une catégorie/class à la nouvelle information mais plutôt comment diviser nos données en catégories/classes (segments, clusters).

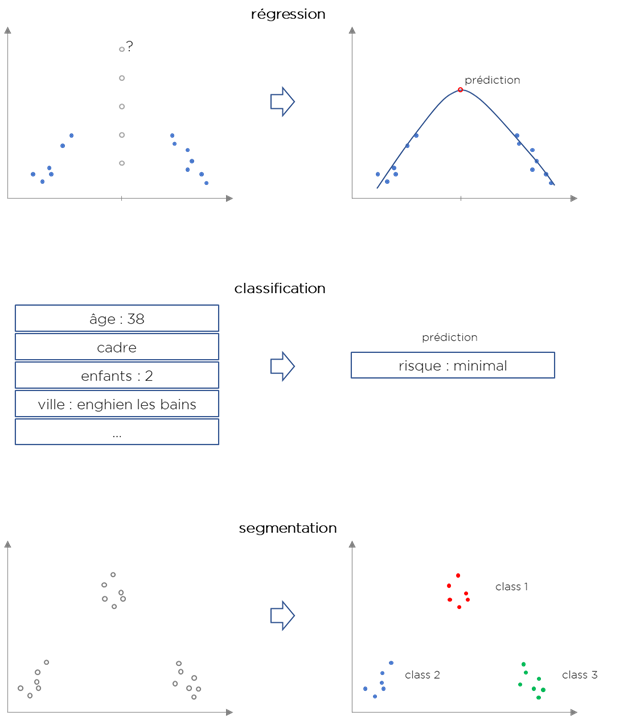
Il existe d’autres types de problèmes, mais démarrons par ces 3. Si vous regardez attentivement, la régression et la classification sont très différentes de la segmentation.

• La régression et la classification doivent s’inspirer des exemples qu’on leur propose et essayer de continuer à faire « aussi bien » sur des données encore jamais vus. C’est un apprentissage supervisé (supervised learning).
• La segmentation crée des classes à partir des données sans n’avoir vu aucun exemple de class. C’est un apprentissage non-supervisé (unsupervised learning).

La notion d’erreur/objectif (objective function, error function, loss function) est très importante dans le Machine Learning.

Supposons que nous avons un certain nombre de données observées (les points) et deux résultats de régression de même jeux de données (« a » et « b » sur l’image ci-dessous). Nous pouvons voir que le résultat « a » « passe mieux » par les données que les résultat « b ». La fonction d’erreur (ou d’objectif) permet de mesurer cette qualité.

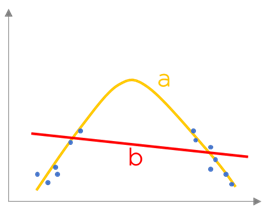
Par exemple, pour la régression la fonction d’erreur est (presque toujours) la suivante :

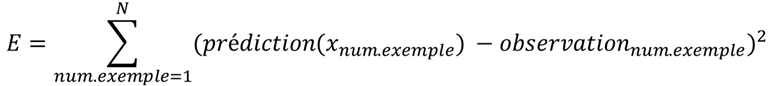
I.e. c’est la somme des carrés de différences de ce que notre modèle prédit et de ce que nous observons dans nos exemples connus. La façon d’écrire cette fonction provient de la théorie de probabilité (c’est un logarithme d’erreur qui suit la loi normale).

Pour la classification, la fonction d’erreur sera différente. La classification prédit pour chaque exemple plusieurs valeurs – autrement dit, la probabilité d’appartenance à chaque classe :

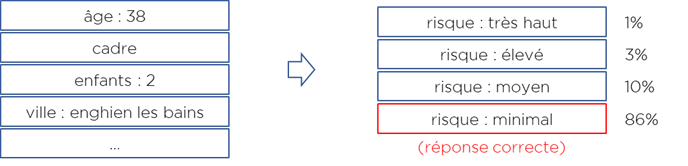
Dans ce cas, la fonction d’erreur appelée « cross-entropie » peut être appliquée (encore une fois la preuve reste dans la théorie de probabilité) :

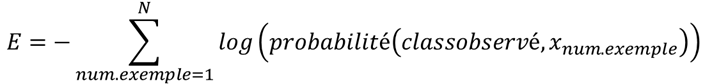
I.e. c’est (moins) une somme de logarithmes de probabilités assignés par notre modèle aux classes correctes. Pour l’exemple précédent pour la réponse correcte le modèle assigne 86% de probabilité, donc l’erreur de ce cas est E=-log(0.86).

Où en sommes-nous ? Pour obtenir un modèle ML, il faut :

• comprendre le problème.
• identifier le type de modèle dont nous avons besoin : régression / classification / segmentation ou autre.
• formuler une fonction d’erreur (objectif) ou prendre une déjà existante,
• choisir l’un des modèles existants (réseaux de neurones, SVM, XGBoost, etc).
• chercher les paramètres de notre modèle afin de trouver une configuration qui minimise l’erreur (fonction d’erreur) – ce dernier processus est la partie learning (apprentissage ou entrainement) :

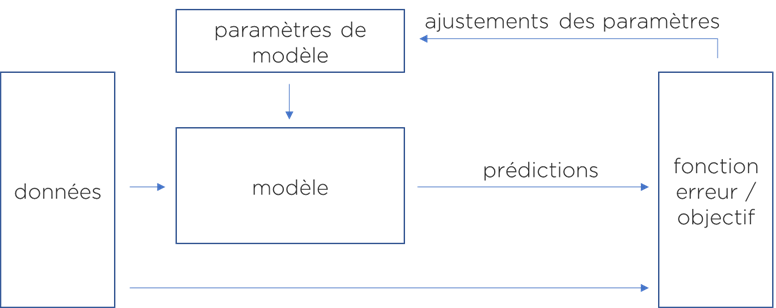
Est-ce tout ? Oh, si seulement …

Prenons un autre exemple – pensez vous que le modèle « c » est meilleur que le modèle « a » ? Il nous semble que la réponse est « non », mais pourquoi ? La fonction d’erreur égale à zéro dit que « c » explique les données mieux que n’importe quel autre modèle (il passe notamment par tous les points que nous avons donné, que voulez-vous).

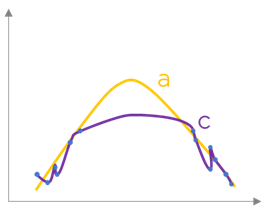
En effet, si nous possédons des données que nous n’avons pas utilisé dans la construction du modèle (nous les aurions mises de côté par exemple), nous pouvons tester les modèles « a » et « c » sur ce nouveau jeu de données. Il est fort probable qu’on trouvera que le modèle « a » fonctionne mieux que le modèle « c ».

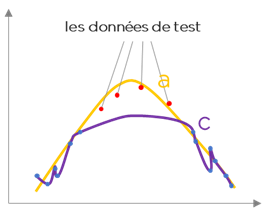
Nous pouvons énoncer que le modèle « c » n’arrive pas à généraliser ou bien possède une faible capacité prédictive ou encore qu’il surapprend (overfit).

Pour cette raison, voici la règle générale : pour vérifier si modèle est suffisamment bon ou pas, nous testons nos modèles sur un jeu de données test qui n’appartient pas au jeu de données d’apprentissage.

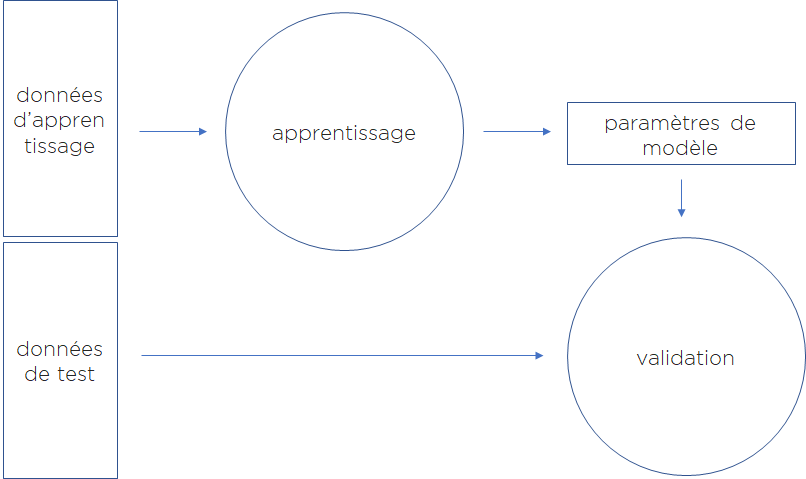
Le problème du surapprentissage est important et prioritaire avant même l’obtention d’un modèle qui minimise l’erreur.

Pour obtenir un modèle qui généralise correctement (et donc pourra être utile), i.e. qui ne surapprend pas, nous introduisons une pénalité qui permettra de « punir » un modèle s’il s’avère trop complexe. Cette punition s’appelle la régularisation. L’idée est la même que dans le fameux rasoir d’Ockham – plus simple l’explication est, mieux c’est.

Comment cela fonctionne-t-il ?

Il existe un nombre considérable de méthodes de régularisation : arrêt précoce d’apprentissage, utilisation de méthodes spécialisées d’apprentissage (ex. SGD / stochastic gradient descent), régularisation L1/L2, dropout, régularisation sur la régularité (oups, désolé), etc. Les autres approches qui ne sont pas tout-à-fait-régularisation, mais qui jouent le même rôle : augmentation de données, boosting/bagging, etc.

Pour notre exemple, on peut utiliser la régularisation L2 (la plus classique). Nous allons ajouter dans notre erreur un supplément suivant (n’ayez pas peur – c’est juste la somme des carrés des paramètres de modèle) :

Cela nous donne la fonction d’erreur suivante :

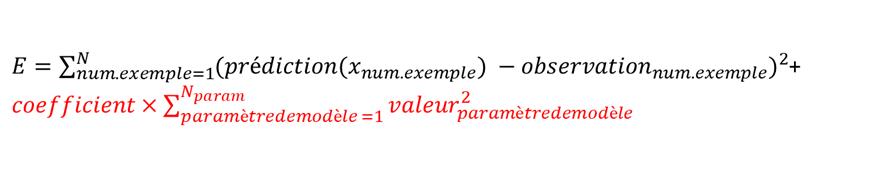
Seul inconvénient : il nous faut maintenant trouver le coefficient de régularisation qui vient d’apparaître. Pour cela, on divise encore nos données pour obtenir cette fois 3 morceaux (on en avait 2) :

• données d’apprentissage – pour trouver les paramètres du modèle.
• données d’optimisation (tuning) des hyper-paramètres – c’est un joli mot pour énoncer « les autres coefficients qui ne font pas directement partie du modèle » (par exemple – notre coefficient de régularisation).
• données de test – pour vérifier le modèle.

Nous ne pouvons pas laisser notre modèle choisir le coefficient de régularisation dans le processus d’optimisation car sinon il va le mettre à zéro – et surapprendra encore une fois (il est paresseux on vous le concède).

Du coup, nous allons obtenir une optimisation à l’intérieur d’une autre optimisation : on va chercher un coefficient de régularisation qui réalise le processus d’apprentissage (sur les données d’apprentissage) tout en produisant le « meilleur modèle » (sur les données d’optimisation des hyper-paramètres).

Voici notre schéma méthodologique « facile à comprendre » :

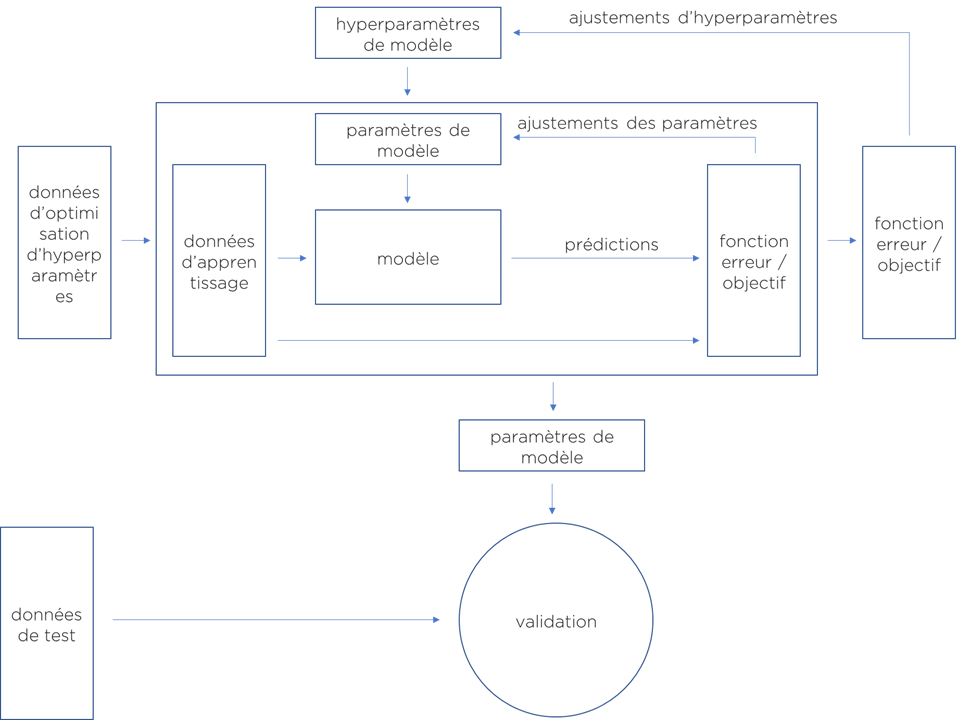
Si vous avec survécu jusqu’ici, vous comprenez le ML mieux que 80% des data scientists que je connais. Vous pouvez vous dire qu’ils connaissent les algorithmes, mais en réalité, ils utilisent simplement Python en ayant une vague idée de ce qui se passe sous le capot.

Une autre difficulté survient quand nous travaillons sur les problèmes complexes : le fléau de la dimension.

Afin d’estimer correctement les paramètres de notre modèle, nous devons disposer de « suffisamment de données ». Par contre, si nous analysons 200/2000/20000 indicateurs dans le modèle, nous avons donc des milliers voire des millions de paramètres, il nous faut vraiment beaucoup de données (pour la plupart d’algorithmes). Ce n’est pas le problème de les stocker (grâce à Hadoop), le problème c’est la source : où prendre autant d’exemples ? Si idéalement pour chaque indicateur nous voulons avoir au moins deux exemples (indépendamment d’autres indicateurs) c’est encore viable quand il y a 10 indicateurs – ça fera 1024 exemples, mais quand on parle de 200 indicateurs, il nous faut « idéalement » 1 606 938 044 258 990 275 541 962 092 341 162 602 522 202 993 782 792 835 301 376 exemples.

Nous avons plusieurs solutions, mais l’une des plus connues – réduction de la dimensionnalité. Le but est de préserver un maximum d’information concernant nos données tout en diminuant le nombre d’indicateurs (paramètres) qu’il nous faut.

Comment cela fonctionne-t-il ?

Supposons que nous avons des données de très haute dimension (par exemple, si nous traitons les images, nous avons probablement un chiffre par pixel (pour décrire l’image en noir et blanc) et même si la résolution est 28×28 pixels, nous avons 784 paramètres ! Est-ce que nous pouvons les réduire à seulement 2 ? En fait, oui, on va évidemment perdre une partie de l’information, mais les résultats sont assez incroyables (https://colah.github.io/posts/2014-10-Visualizing-MNIST/) : vous pouvez visuellement distinguer les classes des chiffres écrites à la main sans faire aucun « machine learning » ! Tout cela pour un problème perçu comme complexe il y a encore 20 ans :

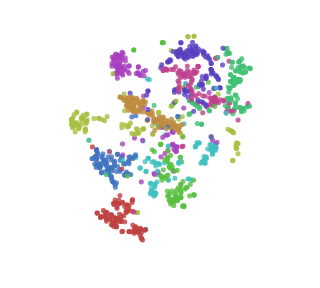
Conclusion

Le Machine Learning est une discipline très intéressante. ML nous aide à résoudre des problèmes complexes avec des algorithmes relativement simple à comprendre. Nous avons essayé de vous donner une visibilité sur les approches et les problèmes du ML. Si ce type d’analyse vous intéresse, ou bien vous souhaitez approfondir, laissez-nous un message et suivez nos prochains posts !

Bonne santé à vous et à vos modèles.