Le théorème de Bayes appliqué à l’archéologie [2/2]

Cet article est la 2nde partie d’article sur une découverte incroyable en Egypte et les probabilités que l’égyptologie soit erronée (https://ithealth.io/la-theorie-bayesienne-appliquee-a-larcheologie-1-2/).

Pour rappel, au XIX siècle Flinders Pétrie découvre un artéfact incroyable – Cylindre Numéro 7 qui semble être une preuve que les égyptiens il y a 2’000 ans ont eu l’accès aux technologies inimaginables.

Pour juger cette découverte, nous nous sommes plongés dans la théorie de probabilités pour découvrir les formules suivantes (pour rappel « | » veut dire « à la condition que… ») :

• P(A)+P(B)=1, si nous savons que A et B couvrent toutes possibilités ;
• P(X) = P(X|A) x P(A) + P(X|B) x P(B), i.e. la probabilité peut être décomposée ;
• P(X|Y) x P(Y) = P(Y|X) x P(X) – théorème de Bayes, i.e. la probabilité peut être inversée.

Mon avis sur l’égyptologie…

Pour détailler et surtout expliquer notre avis sur la question, nous allons comparer les probabilités que l’histoire égyptienne telle qu’elle est décrite dans les livres est plus ou moins correcte (Hist. Classique) versus la probabilité de l’histoire alternative (Hist. Alt.), i.e. l’impacte d’origine extraterrestre / atlantes / etc.

Nous pouvons remarquer que comme avec nos carrés bleus et rouges, la somme des deux probabilités est égale à 1 :

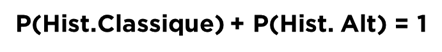
La question est la suivante : en apprenant les résultats de Pétrie, est-ce que nous devons continuer de croire en l’histoire classique ou penchons-nous vers l’histoire alternative ?

Pour décortiquer ce problème, appliquons le théorème de Bayes en inversant le problème :

Maintenant, allons trouver ensemble la probabilité qu’une personne comme Pétrie insiste sur les propriétés étranges de sa trouvaille à la condition que l’histoire classique soit quand même vraie.

Nous pouvons obtenir une formule pour l’histoire alternative aussi (vous allez voir que c’est utile pour la suite) :

Nous pouvons maintenant diviser une formule par une autre – peu importe l’ordre. L’objectif est d’enlever le paramètre P(Pétri) qui est la probabilité que Pétri dit ce qu’il dit dans l’ensemble de mondes possibles. Nous ne savons pas estimer cette probabilité, mais nous n’en n’avons pas besoin non plus, regardez :

Ce que nous avons à gauche c’est le ratio de probabilité d’histoire classique sur la probabilité de d’histoire alternative (si on l’a, on peut répondre à notre question car si ce ratio est supérieur à 1, l’histoire classique est alors la plus probable, si non on peut commencer à croire en l’histoire alternative). En revanche, l’expression à droite nécessite un peu de travail..

Pourquoi Pétri peut dire ce qu’il a dit si l’histoire classique est réelle ? Pour répondre à cette question, nous allons ajouter encore un paramètre : « Pétri croyait à ce qu’il a dit » vs « Pétri ne croyait pas à ce qu’il a dit ». Dans ce cas vu que nous couvrons encore l’ensemble de possibilités, nous pouvons écrire que :

Nous pouvons maintenant interpréter la formule et la décomposer comme vous le voyez dans le schéma ci-dessus.

Posons-nous la question : quelle est la chance qu’un archéologue reconnu fasse une erreur et quelle est la chance qu’il mente délibérément ? Pour ne pas accuser qui que ce soit, prenons des probabilités très basses (1/10’000 ça ira très bien, c’est même trop bas).

Il nous reste deux probabilités difficiles à estimer, mais je ne veux pas dire qu’un archéologue ne croit pas en l’histoire classique et je ne veux pas non plus dire qu’il ment, donc je vais mettre les deux probabilités à 0,5 (cela ne changera pas beaucoup la suite de nos réflexions).

Si l’histoire alternative est correcte et que Pétri a trouvé l’un des premiers artéfacts qui la prouvent, donc :

Remettons tout ensemble pour voir notre résultat intermédiaire (« ~ » c’est « presque ») :

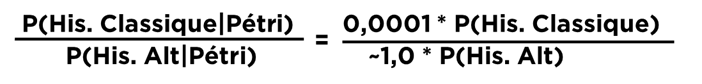
Maintenant tout dépend si vous croyez déjà en histoire alternative ou pas (votre « a priori », i.e. l’avis que vous avez eu avant avoir appris de travaux de Pétri) :

Voici deux possibilités :

• Vous pensez qu’il est improbable que l’histoire alternative soit correcte :
  • P(His. Classique) = 0,9999999, P(His. Alt) = 0,0000001
  • donc P(His. Classique) / P(His. Alt) = 9999999,
  • le résultat finale est 999,9999, donc l’histoire classique reste presque 1000 fois plus probable que l’histoire alternative et vous commencez à croire que Pétri a dû se tromper…
    (« Extraordinary claims require extraordinary evidence », Carl Sagan).
• Vous pensez déjà que les Égyptiens ont eu des contacts avec des extraterrestres, ou tout autre scénario, donc :
  • P(His. Classique) = 0,01, P(His. Alt) = 0,99
  • donc P(His. Classique) / P(His. Alt) = 0,0101…
  • le résultat final est 0,00000101, i.e. maintenant après avoir lu l’information concernant les découvertes de Pétri, pour vous l’histoire alternative est presque 1’000’000 fois plus probable que l’histoire classique. Vous serez encore plus à même de croire que les anciens connaissait des technologies incroyables, etc…

Conclusion : l’information donnée par Pétrie est importante, mais votre « a priori » a encore plus de valeur…

Tout le monde ment

Heureusement pour nous, dans l’archéologie il existe une branche expérimentale. Ci-dessous, vous pouvez voir un trou fait au XXI siècle en utilisant les technologies d’anciens Égyptiens (sans prendre en compte l’histoire alternative).

Sur la photo, vous pouvez voir des traces sur le bois et sur la pierre postérieures à l’utilisation d’abrasifs (pour information, les abrasifs sont nécessaires car les outils ne font pas tout seuls et c’est l’abrasif qui permet la création du trou) :

Par contre, les traces ne sont pas si « parfaites ». En effet, leur origine n’est pas celle qui a été imaginée par Pétri et son conseiller. En cas de manque d’abrasif, les particules ne se dispersent pas partout dans le trou, mais s’agglomèrent au hasard et laissent des traces irrégulières (donc ce ne sont pas les traces de l’instrument comme l’avait suggéré Pétri, mais bien les restes de l’abrasif).

… mais Pétri ne parlait-il pas de traces régulières ?

En fait, vous pouvez vous rendre en Angleterre et constater par vous mêmes l’irrégularité des traces dans le Cylindre Numéro 7. Vous vous rendrez compte que la force de la confiance en soi (l’auto persuasion) peut être cruciale… et même les meilleurs chercheurs peuvent se tromper…

Bonne santé à vous et à vos idées.